题目内容

5．如图，图中所有的三角形都是直角三角形，四边形都是正方形，其中最大正方形E的边长为10，则四个正方形A，B，C，D的面积之和为100．

分析 根据正方形的性质和勾股定理的几何意义解答即可．

解答 解：根据勾股定理的几何意义，可知：
SE=SF+SG
=SA+SB+SC+SD
=100；
即四个正方形A，B，C，D的面积之和为100；
故答案为：100．

点评 本题考查了正方形的性质、勾股定理的几何意义，关键是掌握两直角边的平方和等于斜边的平方．

练习册系列答案
相关题目
11．抛物线y=$\frac{1}{2}{x}^{2}$，y=x2，y=-x2的共同性质是：
①都是开口向上；
②都以点（0，0）为顶点；
③都以y轴为对称轴；
④都关于x轴对称．
其中正确的个数有（　　）
A．1个B．2个C．3个D．4个
16．在△ABC中，∠C=90°，∠B=30°，边AB的垂直平分线交AB于点E，交BC于点D，连接AD，CD=3cm，则BD的长为6cm．
13．计算（a4b）2÷a2的结果是（　　）
A．a2 b2B．a6 b2C．a7 b2D．a8 b2
20．矩形两条对角线的夹角为60°，其中矩形中较短的边长为5，则矩形对角线的长为10．
10．不等式3x-2＞1的解是x＞1．
17．分式方程$\frac{2x+1}{3-x}$=1的解是（　　）
A．x=-$\frac{1}{2}$B．x=2C．x=3D．x=$\frac{2}{3}$
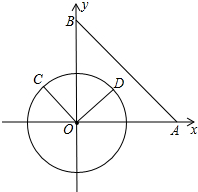14．在平面直角坐标系xOy中，已知点A（8，0），点B（0，8），动点在以半径为4的⊙O上，连接OC，过O点作OD⊥OC，OD与⊙O相交于点D（其中点C、O、D按逆时针方向排列），连接AB．
（1）当OC∥AB时，∠BOC的度数为45°；
（2）连接AC，BC，当点C在⊙O上运动到什么位置时，△ABC的面积最大？并求出△ABC的面积的最大值．
（3）连接AD，当OC∥AD时，
①求出点C的坐标；
②直线BC是否为⊙O的切线？请作出判断，并说明理由．
15．-2的倒数是（　　）
A．2B．-2C．0D．-$\frac{1}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网