题目内容
2.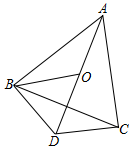 如图,△ABC中,AB=BC,点O是△ABC内一点,将△ABO旋转后能与△BCD重合
如图,△ABC中,AB=BC,点O是△ABC内一点,将△ABO旋转后能与△BCD重合(1)旋转中心是点B;
(2)若∠ACB=70°,旋转角是40度;
(3)若∠ACB=60°,请判断△BOD的形状并说明理由.
分析 (1)根据题意即可得到结论;
(2)根据等腰三角形的性质得到∠BAC=∠ACB=70°,根据三角形的内角和得到∠ABC=180°-∠BAC-∠ACB=40°,根据旋转的性质即可得到结论;
(3)由已知条件得到△ABC是等边三角形,根据等边三角形的性质得到∠ABC=60°,由旋转的性质得到BD=BO,根据等边三角形的判定定理即可得到结论.
解答 解:(1)旋转中心是点B,
故答案为:B;
(2)∵AB=BC,
∴∠BAC=∠ACB=70°,
∴∠ABC=180°-∠BAC-∠ACB=40°,
∵将△ABO旋转后能与△BCD重合,
∴∠ABO=∠CBD,
∴∠OBC+∠ABO=∠OBC+∠CBD=∠ABC=40°,
∵旋转角是40度,
故答案为:40;
(3)△BOD是等边三角形,
∵AB=BC,∠ACB=60°,
∴△ABC是等边三角形,
∴∠ABC=60°,
∵将△ABO旋转后能与△BCD重合,
∴BD=BO,
∵∠OBD=∠ABC=60°,
∴△BOD是等边三角形.
点评 本题考查了旋转的性质,等边三角形的判定和性质,熟练掌握旋转的性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.在有理数中最大的负整数、最小的正整数、绝对值最小的数分别是( )
| A. | -1、0、-1 | B. | 无、1、0 | C. | -1、1、0 | D. | 均无 |
14.下列说法中正确的有( )
①±2都是8的立方根;
②$\sqrt{16}$=±4;
③$\frac{1}{25}$的平方根是±$\frac{1}{5}$;
④-$\root{3}{-8}$=2
⑤-9是81的算术平方根.
①±2都是8的立方根;
②$\sqrt{16}$=±4;
③$\frac{1}{25}$的平方根是±$\frac{1}{5}$;
④-$\root{3}{-8}$=2
⑤-9是81的算术平方根.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.水池中的水位在某天八个不同时间测得的记录如下:(规定与前一天相比上升为正,单位:cm)+3,-6,-1,+5,-4,+2,-3,-2,那么这天水池中水位的最终变化情况是( )
| A. | 上升6cm | B. | 下降6cm | C. | 没升没降 | D. | 下降26cm |

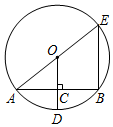 如图,如AE是⊙O的直径,半径OD垂直于弦AB,垂足为C,AB=8cm,CD=2cm,则BE=6cm.
如图,如AE是⊙O的直径,半径OD垂直于弦AB,垂足为C,AB=8cm,CD=2cm,则BE=6cm. 已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.求证:AB=AC.
已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.求证:AB=AC.