题目内容
13．
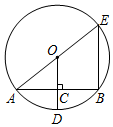如图，如AE是⊙O的直径，半径OD垂直于弦AB，垂足为C，AB=8cm，CD=2cm，则BE=6cm．
分析 根据垂径定理可得AC=4cm，然后设CO=xcm，则DO=AO=（x+2）cm，再利用勾股定理可得（x+2）2=42+x2，解出x的值，再根据三角形中位线定理可得答案．
解答 解：∵半径OD垂直于弦AB，垂足为C，AB=8cm，
∴AC=4cm，
设CO=xcm，则DO=AO=（x+2）cm，
在Rt△AOC中：AO2=CO2+AC2，
∴（x+2）2=42+x2，
解得：x=3，
∵AO=EO，AC=CB，
∴BE=2CO=6cm，
故答案为：6cm．
点评 此题主要考查了垂径定理、勾股定理，以及三角形的中位线定理，关键是掌握三角形的中位线平行于第三边，并且等于第三边的一半；垂直弦的直径平分这条弦，并且平分弦所对的两条弧．
练习册系列答案
相关题目
已知四边形ABCD中，∠B=90°，AB=3，BC=4，CD=$\sqrt{21}$，AD=2，试判断A、B、C、D四点是否在同一个圆上，并说明理由．
1．下列图形不是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
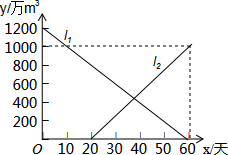今年夏天，重庆各区持续高温日数达到历史之最，受持续高温和连日无雨的影响，重庆某水库的蓄水量随时间的增加而减少，已知原有蓄水量y1（万m3）与干旱持续时间x（天）的关系如图中线段l1所示，针对这种干旱情况，从第20天开始向水库注水，注水量y2（万m3）与时间x（天）的关系如图中线段l2所示（不考虑其他因素）．若总蓄水量不多于900万m3为严重干旱，则该水库发生严重干旱时的天数为15≤x≤40天．
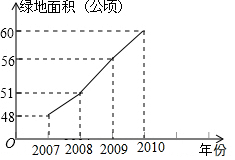美化城市，改善人们的居住环境已成为城市建设的一项重要内容．某市城区近几年来，通过拆迁旧房、植树、种草、修建公园等措施，使城区绿地面积不断增加（如图所示）．
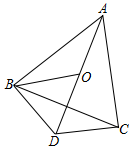如图，△ABC中，AB=BC，点O是△ABC内一点，将△ABO旋转后能与△BCD重合