题目内容
7. 如图,直线l上有A,B,C三点,AB=8cm,l上有两个动点P,Q,点P从点A出发,以$\frac{1}{2}$cm/s的速度沿AB方向运动,同时点Q从点B出发,以$\frac{1}{5}$cm/s的速度沿BC方向运动.
如图,直线l上有A,B,C三点,AB=8cm,l上有两个动点P,Q,点P从点A出发,以$\frac{1}{2}$cm/s的速度沿AB方向运动,同时点Q从点B出发,以$\frac{1}{5}$cm/s的速度沿BC方向运动.(1)当点P,Q出发几秒时,B是线段PQ的中点?
(2)运动过程中,点P和点Q能否重合?若能重合,几秒后重合?
(3)运动过程中,线段PQ与线段AQ的长度能否相等?说明你的理由.
分析 (1)设点P、Q出发t秒钟后,点B是线段PQ的中点.根据题意得到等量关系:BP=BQ;
(2)假设点P、Q出发t秒钟后,点P和点Q重合,则AB+BQ=AP;
(3)需要分类讨论:当点P在点Q左侧和右侧两种情况下的t的值.
解答 解:(1)设点P、Q出发t秒钟后,点B是线段PQ的中点,则
8-$\frac{1}{2}$t=$\frac{1}{5}$t
解得:t=$\frac{80}{7}$,
即点P、Q出发$\frac{80}{7}$秒钟后,点B是线段PQ的中点;
(2)假设点P、Q出发t秒钟后,点P和点Q重合,则
8+$\frac{1}{5}$t=$\frac{1}{2}$t.
解得:t=$\frac{80}{3}$;
(3)当点P在点Q左侧时,线段PQ与线段AQ的长度不可能相等.
当点P在点Q右侧时,设点P、Q出发t秒钟后,线段PQ与线段AQ的长度相等,则
8+$\frac{1}{5}$t=$\frac{1}{2}$t-(8+$\frac{1}{5}$t),
解得:t=160.
当t=160时,线段PQ与线段AQ的长度相等.
点评 本题考查了一元一次方程的应用,数轴,列代数式,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
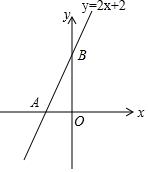 如图所示,直线y=2x+2与x轴交于点A,与y轴交于点B.
如图所示,直线y=2x+2与x轴交于点A,与y轴交于点B.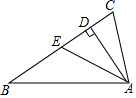 如图,在△ABC中,∠CAB=90°,AD⊥BC,AE是BC边上的中线,4DE=BC,求∠C的度数.
如图,在△ABC中,∠CAB=90°,AD⊥BC,AE是BC边上的中线,4DE=BC,求∠C的度数.