题目内容
2.m为什么整数时,方程mx=4-x的解为正整数?分析 表示出方程的解,根据x为正整数确定出整数m的值即可.
解答 解:方程整理得:x=$\frac{4}{m+1}$,
由x为正整数,得到m+1=-1或-4或1或4或-2或2,
解得:m=-2,-5,0,3,-3,1.
点评 此题考查了一元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.

练习册系列答案
相关题目
13.若多项式(x2-$\frac{1}{3}$xy)-(2y2-3kxy+5)中不含xy项,则k的值为( )
| A. | 1 | B. | -1 | C. | $\frac{1}{9}$ | D. | -$\frac{1}{9}$ |
7. 如图,直线l1与l2相交于点O,OM⊥l1,若β=44°,则α为( )
如图,直线l1与l2相交于点O,OM⊥l1,若β=44°,则α为( )
 如图,直线l1与l2相交于点O,OM⊥l1,若β=44°,则α为( )
如图,直线l1与l2相交于点O,OM⊥l1,若β=44°,则α为( )| A. | 44° | B. | 45° | C. | 46° | D. | 56° |
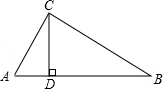 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若∠B=30°,CD=6,求AB的长.
如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若∠B=30°,CD=6,求AB的长. 如图,直线l上有A,B,C三点,AB=8cm,l上有两个动点P,Q,点P从点A出发,以$\frac{1}{2}$cm/s的速度沿AB方向运动,同时点Q从点B出发,以$\frac{1}{5}$cm/s的速度沿BC方向运动.
如图,直线l上有A,B,C三点,AB=8cm,l上有两个动点P,Q,点P从点A出发,以$\frac{1}{2}$cm/s的速度沿AB方向运动,同时点Q从点B出发,以$\frac{1}{5}$cm/s的速度沿BC方向运动.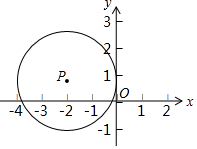 如图,在直角坐标系中,点P的坐标为(-2,1),⊙P与y轴相切,求⊙P在x轴上截得的弦长.
如图,在直角坐标系中,点P的坐标为(-2,1),⊙P与y轴相切,求⊙P在x轴上截得的弦长.