Question

12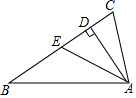．如图，在△ABC中，∠CAB=90°，AD⊥BC，AE是BC边上的中线，4DE=BC，求∠C的度数．

Answer 1

分析 先根据直角三角形斜边上的中线等于斜边的一半得出AE=BE=CE=$\frac{1}{2}$BC，即BC=2CE，再根据4DE=BC，得出CD=DE，又AD⊥BC，根据线段垂直平分线的性质得出AC=AE，那么△ACE是等边三角形，进而求出∠C=60°．

解答 解：∵在△ABC中，∠CAB=90°，AE是BC边上的中线，
∴AE=BE=CE=$\frac{1}{2}$BC，
∴BC=2CE，
∵4DE=BC，
∴CE=2DE，
∴CD=DE，
∵AD⊥BC，
∴AC=AE，
∴AE=CE=AC，
∴△ACE是等边三角形，
∴∠C=60°．

点评 本题考查了直角三角形斜边上的中线的性质：在直角三角形中，斜边上的中线等于斜边的一半．也考查了线段垂直平分线的性质，等边三角形的判定与性质．