题目内容
证明:两个弦切角所夹的弧相等,那么这两个弦切角也相等.
考点:弦切角定理
专题:证明题
分析:首先作出图形,写出已知和求证、根据弦切角定理:弦切角等于同弧所对的圆周角,即可证明.
解答: 已知:AB和DF都是⊙O的切线,切点分别是A和D.
已知:AB和DF都是⊙O的切线,切点分别是A和D.
=
,
求证:∠BAC=∠EDF
证明:在圆上取点F,连接FA、FC、FD、FE.
∵
=
,
∴∠AFC=∠DFE,
又∵AB和DF都是⊙O的切线,
∴∠BAC=∠AFC,∠EDF=∠DFE,
∴∠BAC=∠EDF.
 已知:AB和DF都是⊙O的切线,切点分别是A和D.
已知:AB和DF都是⊙O的切线,切点分别是A和D. |
| AC |
 |
| DE |
求证:∠BAC=∠EDF
证明:在圆上取点F,连接FA、FC、FD、FE.
∵
 |
| AC |
 |
| DE |
∴∠AFC=∠DFE,
又∵AB和DF都是⊙O的切线,
∴∠BAC=∠AFC,∠EDF=∠DFE,
∴∠BAC=∠EDF.
点评:本题考查了弦切角定理,证明命题正确时,要注意证明的格式.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 如图所示,某水库大坝的横断面是梯形,坝顶AD宽2.5m,坝高4m,背水坡的坡度是1:1,迎水坡的坡度是1:1.5,求坝底宽BC.
如图所示,某水库大坝的横断面是梯形,坝顶AD宽2.5m,坝高4m,背水坡的坡度是1:1,迎水坡的坡度是1:1.5,求坝底宽BC.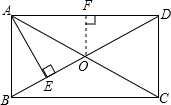 如图,在矩形ABCD中,对角线AC、BD交于点O,自点A作AE⊥BO于点E,且BE:ED=1:3,过点O作OF⊥AD于点F,若OF=3cm,求BD的长.
如图,在矩形ABCD中,对角线AC、BD交于点O,自点A作AE⊥BO于点E,且BE:ED=1:3,过点O作OF⊥AD于点F,若OF=3cm,求BD的长. 如图,点P为圆上的一个动点,弦AB=
如图,点P为圆上的一个动点,弦AB= 如图,在△ABC中,D为AB边上一点、F为AC的中点,过点C作CE∥AB交DF的延长线于点E,连结AE.
如图,在△ABC中,D为AB边上一点、F为AC的中点,过点C作CE∥AB交DF的延长线于点E,连结AE.