题目内容
已知方程x2-mx+45=0的两个实数根的差的平方为144,则m= .
考点:根与系数的关系,根的判别式
专题:计算题
分析:设方程的两根分别为a、b,根据根与系数的关系得到a+b=m,ab=45,利用完全平方公式,由(a-b)2=144得到(a+b)2-4ab=144,则m2-4×45=144,解得m1=18,m2=-18,然后根据判别式的意义确定m的值.
解答:解:设方程的两根分别为a、b,则a+b=m,ab=45,
∵(a-b)2=144,
∴(a+b)2-4ab=144,
∴m2-4×45=144,
解得m1=18,m2=-18,
∵当m=±18时,△=m2-4×45>0,
∴m的值为18或-18.
故答案为18或-18.
∵(a-b)2=144,
∴(a+b)2-4ab=144,
∴m2-4×45=144,
解得m1=18,m2=-18,
∵当m=±18时,△=m2-4×45>0,
∴m的值为18或-18.
故答案为18或-18.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.也考查了根的判别式.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
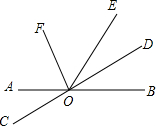 如图,直线AB,CD相交于点O,OD平分∠BOE,OF平分∠AOE.
如图,直线AB,CD相交于点O,OD平分∠BOE,OF平分∠AOE.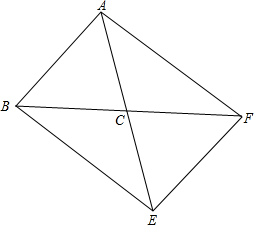 已知,如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△EFC.
已知,如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△EFC.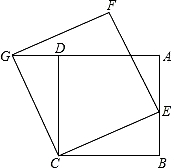 如图,已知正方形ABCD,点E是AB上的一点,连接CE,以CE为一边,在CE的上方作正方形CEFG,连接DG.求证:BE=DG.
如图,已知正方形ABCD,点E是AB上的一点,连接CE,以CE为一边,在CE的上方作正方形CEFG,连接DG.求证:BE=DG. 如图,在菱形ABCD中,过点B作BM⊥AD于点M,BN⊥CD于点N,BM,BN分别交AC于点E、F.求证:AE=CF.
如图,在菱形ABCD中,过点B作BM⊥AD于点M,BN⊥CD于点N,BM,BN分别交AC于点E、F.求证:AE=CF.