题目内容
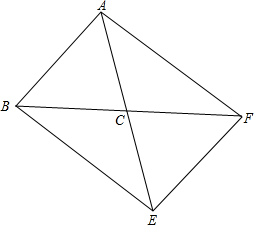 已知,如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△EFC.
已知,如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△EFC.(1)若△ABC的面积为3cm2,求四边形ABEF的面积;
(2)当∠ACB为多少度时,四边形ABFE为矩形?(说明理由)
考点:旋转的性质,矩形的判定
专题:常规题型
分析:(1)根据旋转的性质得AC=CE,BC=CF,可判断四边形ABEF为平行四边形,根据平行四边形的性质即可得到四边形ABEF的面积=4S△ABC=12cm2;
(2)由于四边形ABEF为平行四边形,根据矩形的判定方法,当AE=BF时,四边形ABEF为矩形,则AC=BC,易得AB=BC=AC,所以△ABC为等边三角形,于是得到∠ACB=60°.
(2)由于四边形ABEF为平行四边形,根据矩形的判定方法,当AE=BF时,四边形ABEF为矩形,则AC=BC,易得AB=BC=AC,所以△ABC为等边三角形,于是得到∠ACB=60°.
解答:解:(1)∵△ABC绕点C顺时针旋转180°得到△EFC,
∴AC=CE,BC=CF,
∴四边形ABEF为平行四边形,
∴四边形ABEF的面积=4S△ABC=4×3=12(cm2);
(2)∵四边形ABEF为平行四边形,
∴当AE=BF时,四边形ABEF为矩形,
即AC=BC,
而AB=AC,
∴AB=BC=AC,
∴△ABC为等边三角形,
∴∠ACB=60°,
即当∠ACB为60度时,四边形ABFE为矩形.
∴AC=CE,BC=CF,
∴四边形ABEF为平行四边形,
∴四边形ABEF的面积=4S△ABC=4×3=12(cm2);
(2)∵四边形ABEF为平行四边形,
∴当AE=BF时,四边形ABEF为矩形,
即AC=BC,
而AB=AC,
∴AB=BC=AC,
∴△ABC为等边三角形,
∴∠ACB=60°,
即当∠ACB为60度时,四边形ABFE为矩形.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角.旋转前、后的图形全等.也考查了平行四边形的判定与性质和矩形的判定.

练习册系列答案
相关题目
根据2010年第六次全国人口普查主要数据公报,贵州省常住人口约为4156万人,这一数据可以用科学记数法表示为( )
| A、4.156×107人 |
| B、4.156×106人 |
| C、4156×104人 |
| D、4.156×103人 |
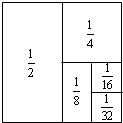 如图所示,将面积为1的长方形等分成两个面积为
如图所示,将面积为1的长方形等分成两个面积为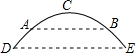 如图是某地一座抛物线形拱桥,桥拱在竖直平面内,与水面相交于A,B两点,拱桥最高点C到AB的距离为9m,AB=36m,D,E为拱桥底部的两点,且DE∥AB,点E到直线AB的距离为7m.建立平面直角坐标系,求:
如图是某地一座抛物线形拱桥,桥拱在竖直平面内,与水面相交于A,B两点,拱桥最高点C到AB的距离为9m,AB=36m,D,E为拱桥底部的两点,且DE∥AB,点E到直线AB的距离为7m.建立平面直角坐标系,求: