题目内容
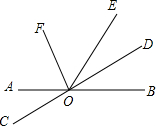 如图,直线AB,CD相交于点O,OD平分∠BOE,OF平分∠AOE.
如图,直线AB,CD相交于点O,OD平分∠BOE,OF平分∠AOE.(1)若∠BOD=28°,求∠DOE和∠FOE的度数;
(2)若改变∠BOD的度数,试猜想∠DOF的度数是否发生改变?若不改变,请直接写出∠DOF的度数,若改变,请说明理由.
考点:角平分线的定义
专题:
分析:(1)根据角平分线的性质可以∠DOE=∠BOD=28°,然后结合邻补角的定义和角平分线的性质来求∠FOE的度数;
(2)根据平角的定义和角平分线的性质推知∠DOF=90°,为定值.
(2)根据平角的定义和角平分线的性质推知∠DOF=90°,为定值.
解答: 解:(1)如图,∵OD平分∠BOE,∠BOD=28°,
解:(1)如图,∵OD平分∠BOE,∠BOD=28°,
∴∠DOE=∠BOD=28°.
∴∠AOE=180°-2∠BOD=124°.
又∵OF平分∠AOE,
∴∠FOE=
∠AOE=62°;
(2)若改变∠BOD的度数,试猜想∠DOF的度数不发生改变.理由如下:
∵OD平分∠BOE,OF平分∠AOE,∠AOE+∠DOE=180°,
∴∠EOF+∠EOD=
(∠AOE+∠DOE)=90°,
即∠DOF=90°.
 解:(1)如图,∵OD平分∠BOE,∠BOD=28°,
解:(1)如图,∵OD平分∠BOE,∠BOD=28°,∴∠DOE=∠BOD=28°.
∴∠AOE=180°-2∠BOD=124°.
又∵OF平分∠AOE,
∴∠FOE=
| 1 |
| 2 |
(2)若改变∠BOD的度数,试猜想∠DOF的度数不发生改变.理由如下:
∵OD平分∠BOE,OF平分∠AOE,∠AOE+∠DOE=180°,
∴∠EOF+∠EOD=
| 1 |
| 2 |
即∠DOF=90°.
点评:本题考查了角平分线的性质.解题时,是根据角平分线定义得出所求角与已知角的关系转化求解.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
 如图所示,在宽为20m,长为32m的矩形地面上,修筑同样宽的三条道路,(互相垂直),余下部分作为耕地,耕地面积为570m2,如果设修建道路的宽为x m,则x满足的方程是( )
如图所示,在宽为20m,长为32m的矩形地面上,修筑同样宽的三条道路,(互相垂直),余下部分作为耕地,耕地面积为570m2,如果设修建道路的宽为x m,则x满足的方程是( )| A、2x2-52x+32=0 |
| B、x2-52x+64=0 |
| C、x2-36x+35=0 |
| D、x2-36x-35=0 |
某超市第二季度的营业额为200万元,第四季度的营业额为288万元.如果每季度营业额的平均增长率相同,那么每季度的平均增长率是( )
| A、10% | B、15% |
| C、20% | D、30% |
根据2010年第六次全国人口普查主要数据公报,贵州省常住人口约为4156万人,这一数据可以用科学记数法表示为( )
| A、4.156×107人 |
| B、4.156×106人 |
| C、4156×104人 |
| D、4.156×103人 |
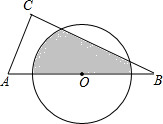 如图,在△ABC中,∠C=90°,AB=6,AC=3,O为AB中点,则半径为
如图,在△ABC中,∠C=90°,AB=6,AC=3,O为AB中点,则半径为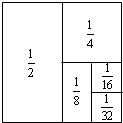 如图所示,将面积为1的长方形等分成两个面积为
如图所示,将面积为1的长方形等分成两个面积为