题目内容
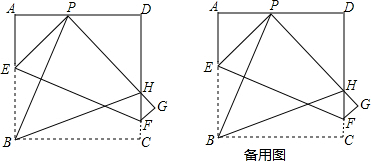
8.如图所示,现有一张边长为4的正方形纸片,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是8;
(3)设AP为x,四边形EFGP的面积为S,求出S与x的函数关系式,试问S是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
分析 (1)根据翻折变换的性质得出∠PBC=∠BPH,进而利用平行线的性质得出∠APB=∠PBC即可得出答案;
(2)首先证明△ABP≌△QBP,进而得出△BCH≌△BQH,即可得出PD+DH+PH=AP+PD+DH+HC=AD+CD=8;
(3)利用已知得出△EFM≌△BPA,进而利用在Rt△APE中,(4-BE)2+x2=BE2,利用二次函数的最值求出即可.
解答 (1)证明:∵PE=BE,
∴∠EBP=∠EPB.
又∵∠EPH=∠EBC=90°,
∴∠EPH-∠EPB=∠EBC-∠EBP.
即∠PBC=∠BPH.
又∵AD∥BC,
∴∠APB=∠PBC.
∴∠APB=∠BPH.
(2)解:如图2,过B作BQ⊥PH,垂足为Q.
由(1)知∠APB=∠BPH,
在△ABP和△QBP中,$\left\{\begin{array}{l}{∠APB=∠BPH}&{\;}\\{∠A=∠BQP}&{\;}\\{BP=BP}&{\;}\end{array}\right.$,
∴△ABP≌△QBP(AAS).
∴AP=QP,AB=BQ.
又∵AB=BC,
∴BC=BQ.
又∵∠C=∠BQH=90°,BH=BH,
∴△BCH≌△BQH.
∴CH=QH.
∴△PHD的周长=PD+DH+PH=AP+PD+DH+HC=AD+CD=8;
故答案为:8.
(3)解:如图3,过F作FM⊥AB,垂足为M,则FM=BC=AB.
又∵EF为折痕,
∴EF⊥BP.
∴∠EFM+∠MEF=∠ABP+∠BEF=90°,
∴∠EFM=∠ABP.
又∵∠A=∠EMF=90°,
∴△EFM≌△PBA(ASA).
∴EM=AP=x.
∴在Rt△APE中,(4-BE)2+x2=BE2.
解得,NE=2+$\frac{{x}^{2}}{8}$.
∴CF=BE+EM=2+$\frac{{x}^{2}}{8}$-x.
又∵折叠的性质得出四边形EFGP与四边形BEFC全等,
∴S=$\frac{1}{2}$(BE+CF)•BC=$\frac{1}{2}$(4+$\frac{{x}^{2}}{4}$-x)×4,
即:S=$\frac{1}{2}$x2-2x+8.
配方得,S=$\frac{1}{2}$(x-2)2+6,
∴当x=2时,S有最小值6.
点评 此题主要考查了翻折变换的性质以及全等三角形的判定与性质和勾股定理、二次函数的最值问题等知识,熟练利用全等三角形的判定得出对应相等关系是解题关键.

 如图,△ABC中,BC=a,AC=b,AB=c(b<c<a),BC的垂直平分线DG交∠BAC的角平分线AD于点D,DE⊥AB于E,DF⊥AC于F,则下列结论一定成立的是( )
如图,△ABC中,BC=a,AC=b,AB=c(b<c<a),BC的垂直平分线DG交∠BAC的角平分线AD于点D,DE⊥AB于E,DF⊥AC于F,则下列结论一定成立的是( )| A. | DG=$\frac{1}{2}$(a+b) | B. | CF=c-b | C. | BE=$\frac{1}{2}$(a-b) | D. | AE=$\frac{1}{2}$(b+c) |
 如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,6),⊙C的半径长为5,则C点坐标为( )
如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,6),⊙C的半径长为5,则C点坐标为( )| A. | (3,4) | B. | (4,3) | C. | (-4,3) | D. | (-3,4) |
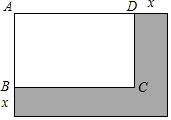 如图,矩形ABCD的长AD=5cm,宽AB=3cm,长和宽都增加xcm,那么面积增加ycm2.
如图,矩形ABCD的长AD=5cm,宽AB=3cm,长和宽都增加xcm,那么面积增加ycm2. 如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…An,…将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:①抛物线的顶点M1,M2,M3,…Mn,…都在直线L:y=x上;②抛物线依次经过点A1,A2,A3…An,…则顶点M2017的坐标为(4033,4033).
如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…An,…将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:①抛物线的顶点M1,M2,M3,…Mn,…都在直线L:y=x上;②抛物线依次经过点A1,A2,A3…An,…则顶点M2017的坐标为(4033,4033).