题目内容
2.在平面直角坐标系中,已知A(-1,2)、B(7,8).若在坐标轴上取点C,使△ABC为直角三角形,则满足条件的C点的个数共有( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 过点A作AB的垂线,交x轴于点C1,交y轴于点C2;过点B作AB的垂线,交x轴于点C3,交y轴于点C4;根据直径所对的圆周角为直角,以AB为直径作圆,根据A和B的坐标求出AB的长度,即为圆的直径,可得出半径的长,进而判断得出圆与x轴相离,可得出圆与y轴交于2点.所以满足条件的点共有6个.
解答 解:分三种情况考虑:当A为直角顶点时,过A作AC⊥AB,交x轴于点C1,交y轴于点C2,此时满足题意的点为C1,C2;
当B为直角顶点时,过B作BC⊥⊥AB,交x轴于点C3,交y轴于点C4,此时满足题意的点为C3,C4;
当C为直角顶点时,以AB为直径作圆,由A(-1,2),B(7,8),可得此圆与x轴相离,
则此圆与x轴没有交点,与y轴有2个交点,分别为C5,C6.
综上,所有满足题意的C有6个.
故选A.
点评 此题考查了圆周角定理,勾股定理,以及坐标与图形性质,利用了分类讨论及数形结合的思想.注意:若△ABC是直角三角形,则它的任意一个顶点都有可能为直角顶点.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
7.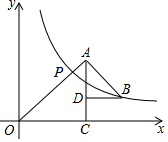 如图所示,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,与OA交于点P,且OA2-AB2=18,则点P的横坐标为( )
如图所示,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,与OA交于点P,且OA2-AB2=18,则点P的横坐标为( )
 如图所示,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,与OA交于点P,且OA2-AB2=18,则点P的横坐标为( )
如图所示,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,与OA交于点P,且OA2-AB2=18,则点P的横坐标为( )| A. | 9 | B. | 6 | C. | 3 | D. | 3$\sqrt{2}$ |
12.不等式4x-8≤0的解集是( )
| A. | x≥-2 | B. | ≤-2 | C. | ≥2 | D. | ≤2 |
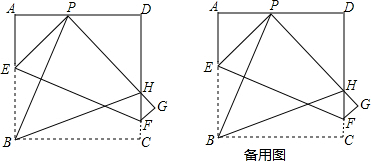

 如图,在等腰直角三角形ABC中,∠ACB=90°,AB=8$\sqrt{2}$cm,点P(不与A,B重合)从点A出发,沿AB方向以$\sqrt{2}$cm/s的速度向终点B运动,在运动过程中,过点P作PQ⊥AB交射线BC于点Q,以线段PQ为边作等腰直角三角形PQR,且∠PQR=90°(点B,R位于PQ两侧),设△PQR与△ABC重叠部分图形的面积为S(cm2),点P的运动时间为t(s).
如图,在等腰直角三角形ABC中,∠ACB=90°,AB=8$\sqrt{2}$cm,点P(不与A,B重合)从点A出发,沿AB方向以$\sqrt{2}$cm/s的速度向终点B运动,在运动过程中,过点P作PQ⊥AB交射线BC于点Q,以线段PQ为边作等腰直角三角形PQR,且∠PQR=90°(点B,R位于PQ两侧),设△PQR与△ABC重叠部分图形的面积为S(cm2),点P的运动时间为t(s).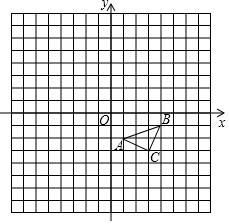 如图.在平面直角坐标系内,△ABC三个顶点的坐标分别为A(1,-2),B(4,-1),C(3,-3)(正方形网格中,每个小正方形的边长都是1个单位长度).
如图.在平面直角坐标系内,△ABC三个顶点的坐标分别为A(1,-2),B(4,-1),C(3,-3)(正方形网格中,每个小正方形的边长都是1个单位长度). 如图,正五边形的边长为2,连接对角线AD、BE、CE,线段AD分别与BE和CE相交于点M、N,给出下列结论:①∠AME=108°,②AN2=AM•AD;③MN=3-$\sqrt{5}$;④S△EBC=2$\sqrt{5}$-1,其中正确的结论是①②③(把你认为正确结论的序号都填上).
如图,正五边形的边长为2,连接对角线AD、BE、CE,线段AD分别与BE和CE相交于点M、N,给出下列结论:①∠AME=108°,②AN2=AM•AD;③MN=3-$\sqrt{5}$;④S△EBC=2$\sqrt{5}$-1,其中正确的结论是①②③(把你认为正确结论的序号都填上).