题目内容
20．
如图，⊙C过原点，且与两坐标轴分别交于点A、点B，点A的坐标为（0，6），⊙C的半径长为5，则C点坐标为（ ）| A． | （3，4） | B． | （4，3） | C． | （-4，3） | D． | （-3，4） |
分析 先求出B点坐标，再由中点坐标的性质即可得出结论．
解答 解：∵⊙C过原点，∠AOB=90°
∴AB是⊙O的直径．
∵点A的坐标为（0，6），⊙C的半径长为5，
∴OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=8，
∴B（-8，0），
∴C（-4，3）．
故选C．
点评 本题考查的是圆周角定理，熟知直径所对的圆周角是直角是解答此题的关键．
练习册系列答案
相关题目
11．在平面直角坐标系中，正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置，其中点B1在y轴上，点C1、E1、E2、C2、E3、E4、C3…在x轴上，已知正方形A1B1C1D1的边长为1，∠B1C1O=60°，B1C1∥B2C2∥B3C3…则正方形A2017B2017C2017D2017的边长是（ ）
| A． | （$\frac{1}{2}$）2014 | B． | （$\frac{1}{2}$）2015 | C． | （$\frac{\sqrt{3}}{3}$）2016 | D． | （$\frac{\sqrt{3}}{3}$）2017 |
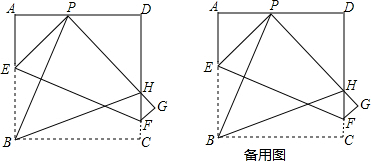
如图，在四边形ABCD中，AB=DC，延长线段CB到E，使BE=AD，连接AE，AC，∠ADC+∠ABC=180°．
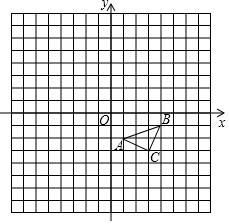如图．在平面直角坐标系内，△ABC三个顶点的坐标分别为A（1，-2），B（4，-1），C（3，-3）（正方形网格中，每个小正方形的边长都是1个单位长度）．