题目内容
13.杨辉是我国南宋末年的一位杰出的数学家.在他著的《详解九章算法》一书中,画了一张表示二项式展开后的系数构成的三角图形,称做“开方做法本源”,现在简称为“杨辉三角”,它是杨辉的一大重要研究成果.我们把杨辉三角的每一行分别相加,如下:
1 ( 1 )
1 1 ( 1+1=2 )
1 2 1 (1+2+1=4 )
1 3 3 1 (1+3+3+1=8 )
1 4 6 4 1 (1+4+6+4+1=16 )
1 5 10 10 5 1 (1+5+10+10+5+1=32 )
1 6 15 20 15 6 1 (1+6+15+20+15+6+1=64 )
…写出杨辉三角第n行中n个数之和等于2n-1.
分析 由题意得出每行的数字之和等于2的序数减一次幂,据此解答即可.
解答 解:∵第1行数字之和1=20,
第2行数字之和2=21,
第3行数字之和4=22,
第4行数字之和8=23,
…
∴第n行数字之和2n-1,
故答案为:2n-1.
点评 本题主要考查数字的变化类,解题的关键是每行的数相加,分析总结得出规律,根据规律求出第n行的数据之和.

练习册系列答案
相关题目
 如图所示,课间操时,小华、小军、小刚的位置如图,小华对小刚说:“如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置应表示为(4,3).”
如图所示,课间操时,小华、小军、小刚的位置如图,小华对小刚说:“如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置应表示为(4,3).”
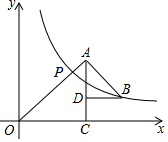 如图所示,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,与OA交于点P,且OA2-AB2=18,则点P的横坐标为( )
如图所示,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,与OA交于点P,且OA2-AB2=18,则点P的横坐标为( )