题目内容
6．
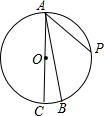如图，AC是⊙O的直径，∠BAC=10°，P是$\widehat{AB}$的中点，则∠PAB的大小是（ ）| A． | 35° | B． | 40° | C． | 60° | D． | 70° |
分析 连接OP，OB，利用圆周角定理得到∠BOC=2∠BAC，求出∠BOC度数，进而求出∠AOB度数，再利用圆心角、弦、弧之间的关系求出所求角度数即可．
解答 
解：连接OP，OB，
∵∠BAC=10°，
∴∠BOC=2∠BAC=20°，
∴∠AOB=160°，
∵P为$\widehat{AB}$的中点，
∴∠BOP=$\frac{1}{2}$∠AOB=80°，
∴∠PAB=40°，
故选B
点评 此题考查了圆周角定理，圆心角、弦、弧之间的关系，熟练掌握圆周角定理是解本题的关键．
练习册系列答案
备战中考寒假系列答案
相关题目
17．下列运算正确的是（ ）
| A． | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | B． | 2$\sqrt{3}$-$\sqrt{3}$=$\sqrt{3}$ | C． | 2+$\sqrt{2}$=2$\sqrt{2}$ | D． | $\sqrt{3}$-$\sqrt{2}$=1 |
14．下列各数：3.14159，0，0.3131131113…（相邻两个3之间1的个数逐次加1），-$\sqrt{256}$，-$\frac{22}{7}$，其中无理数有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
1．从长度分别为2，4，6，8的四条线段中任选三条作边，能构成三角形的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{5}$ |
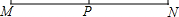如图，已知线段MN═6cm，点P是MN的中点．分别以M、N为圆心，r1cm，r2cm为半径画圆．若点P在⊙M内，又在⊙N外．则r1的范围是r1＞3，r2的范围是0＜r2＜3．