题目内容
11．
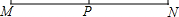如图，已知线段MN═6cm，点P是MN的中点．分别以M、N为圆心，r1cm，r2cm为半径画圆．若点P在⊙M内，又在⊙N外．则r1的范围是r1＞3，r2的范围是0＜r2＜3．
分析 根据点在圆外，点到圆心的距离大于半径的长，点在圆内，点到圆心的距离小于半径可以解答本题．
解答 解：∵MN=6cm，点P是MN的中点，
∴MP=NP=3cm，
∵以M、N为圆心，r1cm，r2cm为半径画圆，点P在⊙M内，又在⊙N外，
∴r2＞3，0＜r2＜3，
故答案为：r2＞3，0＜r2＜3．
点评 本题考查点与圆的位置关系，解题的关键是明确题意，找出所求问题需要的条件．
练习册系列答案
相关题目
2．
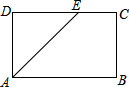如图，在矩形ABCD中，AB=5，BC=3，∠BAD的角平分线与DC交于点E，则CE的长为（ ）
如图，在矩形ABCD中，AB=5，BC=3，∠BAD的角平分线与DC交于点E，则CE的长为（ ）| A． | 2 | B． | 2.5 | C． | 3 | D． | 4 |
19．
一个有进水管与出水管的容器，从某时刻开始4min内只进水不出水，在随后的8min内既进水又出水，每分的进水量和出水量有两个常数，容器内的水量y（单位：L）与时间x（单位：min）之间的关系如图所示．则每分出水（ ）
一个有进水管与出水管的容器，从某时刻开始4min内只进水不出水，在随后的8min内既进水又出水，每分的进水量和出水量有两个常数，容器内的水量y（单位：L）与时间x（单位：min）之间的关系如图所示．则每分出水（ ）| A． | $\frac{15}{4}$升 | B． | 4升 | C． | 5升 | D． | $\frac{25}{4}$升 |
6．
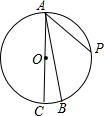如图，AC是⊙O的直径，∠BAC=10°，P是$\widehat{AB}$的中点，则∠PAB的大小是（ ）
如图，AC是⊙O的直径，∠BAC=10°，P是$\widehat{AB}$的中点，则∠PAB的大小是（ ）| A． | 35° | B． | 40° | C． | 60° | D． | 70° |
16．下列各组运算中结果相等的是（ ）
| A． | -24与（-2）4 | B． | （-1）4与（-1）2016 | C． | -（-8）与-|-8| | D． | 52与25 |
