题目内容
1.从长度分别为2,4,6,8的四条线段中任选三条作边,能构成三角形的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
分析 首先根据题意,可列举出所有等可能的结果,又由能构成三角形的只有4,6,8,直接利用概率公式求解即可求得答案.
解答 解:∵从长度分别为2,4,6,8的四条线段中任选三条作边,等可能的结果有:2,4,6; 2,4,8; 2,6,8; 4,6,8;
其中能构成三角形的只有4,6,8;
∴能构成三角形的概率为:$\frac{1}{4}$.
故选C.
点评 此题考查了列举法求概率的知识.注意不重不漏的列举出所有等可能的结果是关键.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
12.如果$\frac{a}{b}$=$\frac{2}{3}$,则$\frac{a+b}{b}$=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{3}$ | D. | $\frac{3}{5}$ |
9. 如图,AB∥l,AB=6,直线AB与l间的距离为4,若点P是直线l上的一动点,则△PAB的周长的最小值为( )
如图,AB∥l,AB=6,直线AB与l间的距离为4,若点P是直线l上的一动点,则△PAB的周长的最小值为( )
 如图,AB∥l,AB=6,直线AB与l间的距离为4,若点P是直线l上的一动点,则△PAB的周长的最小值为( )
如图,AB∥l,AB=6,直线AB与l间的距离为4,若点P是直线l上的一动点,则△PAB的周长的最小值为( )| A. | 12 | B. | 16 | C. | 14 | D. | 18 |
16.在?ABCD中,AB=3,BC=4,AC=5,则?ABCD的面积为( )
| A. | 6 | B. | 12 | C. | 18 | D. | 24 |
6.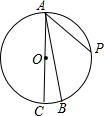 如图,AC是⊙O的直径,∠BAC=10°,P是$\widehat{AB}$的中点,则∠PAB的大小是( )
如图,AC是⊙O的直径,∠BAC=10°,P是$\widehat{AB}$的中点,则∠PAB的大小是( )
 如图,AC是⊙O的直径,∠BAC=10°,P是$\widehat{AB}$的中点,则∠PAB的大小是( )
如图,AC是⊙O的直径,∠BAC=10°,P是$\widehat{AB}$的中点,则∠PAB的大小是( )| A. | 35° | B. | 40° | C. | 60° | D. | 70° |
11. 已知一个由50个偶数排成的数阵.用如图所示的框去框住四个数,并求出这四个数的和.在下列给出备选答案中,有可能是这四个数的和的是( )
已知一个由50个偶数排成的数阵.用如图所示的框去框住四个数,并求出这四个数的和.在下列给出备选答案中,有可能是这四个数的和的是( )
 已知一个由50个偶数排成的数阵.用如图所示的框去框住四个数,并求出这四个数的和.在下列给出备选答案中,有可能是这四个数的和的是( )
已知一个由50个偶数排成的数阵.用如图所示的框去框住四个数,并求出这四个数的和.在下列给出备选答案中,有可能是这四个数的和的是( )| A. | 80 | B. | 148 | C. | 172 | D. | 220 |