题目内容
17.下列运算正确的是( )| A. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | B. | 2$\sqrt{3}$-$\sqrt{3}$=$\sqrt{3}$ | C. | 2+$\sqrt{2}$=2$\sqrt{2}$ | D. | $\sqrt{3}$-$\sqrt{2}$=1 |
分析 结合二次根式的加减法运算法则进行求解即可.
解答 解:A、$\sqrt{3}+\sqrt{2}$≠$\sqrt{5}$,本选项错误;
B、2$\sqrt{3}$-$\sqrt{3}$=$\sqrt{3}$,本选项正确;
C、2+$\sqrt{2}$≠2$\sqrt{2}$,本选项错误;
D、$\sqrt{3}-\sqrt{2}$≠1,本选项错误.
故选B.
点评 本题考查了二次根式的加减法,解答本题的关键在于熟练掌握二次根式加减法运算法则.

练习册系列答案
相关题目
5.已知一组数据3、a、4、5、9的众数是4,则这组数据的平均数是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
12.如果$\frac{a}{b}$=$\frac{2}{3}$,则$\frac{a+b}{b}$=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{3}$ | D. | $\frac{3}{5}$ |
2.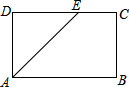 如图,在矩形ABCD中,AB=5,BC=3,∠BAD的角平分线与DC交于点E,则CE的长为( )
如图,在矩形ABCD中,AB=5,BC=3,∠BAD的角平分线与DC交于点E,则CE的长为( )
 如图,在矩形ABCD中,AB=5,BC=3,∠BAD的角平分线与DC交于点E,则CE的长为( )
如图,在矩形ABCD中,AB=5,BC=3,∠BAD的角平分线与DC交于点E,则CE的长为( )| A. | 2 | B. | 2.5 | C. | 3 | D. | 4 |
9. 如图,AB∥l,AB=6,直线AB与l间的距离为4,若点P是直线l上的一动点,则△PAB的周长的最小值为( )
如图,AB∥l,AB=6,直线AB与l间的距离为4,若点P是直线l上的一动点,则△PAB的周长的最小值为( )
 如图,AB∥l,AB=6,直线AB与l间的距离为4,若点P是直线l上的一动点,则△PAB的周长的最小值为( )
如图,AB∥l,AB=6,直线AB与l间的距离为4,若点P是直线l上的一动点,则△PAB的周长的最小值为( )| A. | 12 | B. | 16 | C. | 14 | D. | 18 |
6.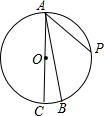 如图,AC是⊙O的直径,∠BAC=10°,P是$\widehat{AB}$的中点,则∠PAB的大小是( )
如图,AC是⊙O的直径,∠BAC=10°,P是$\widehat{AB}$的中点,则∠PAB的大小是( )
 如图,AC是⊙O的直径,∠BAC=10°,P是$\widehat{AB}$的中点,则∠PAB的大小是( )
如图,AC是⊙O的直径,∠BAC=10°,P是$\widehat{AB}$的中点,则∠PAB的大小是( )| A. | 35° | B. | 40° | C. | 60° | D. | 70° |