题目内容
20.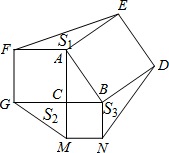 如图,△ABC中,∠ACB=90°,AC>BC,分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,连接EF、GM、ND,设△AEF、△BND、△CGM的面积分别为S1、S2、S3,则下列结论正确的是( )
如图,△ABC中,∠ACB=90°,AC>BC,分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,连接EF、GM、ND,设△AEF、△BND、△CGM的面积分别为S1、S2、S3,则下列结论正确的是( )| A. | S1=S2=S3 | B. | S1=S2<S3 | C. | S1=S3<S2 | D. | S2=S3<S1 |
分析 设直角三角形的三边分别为a、b、c,分别表示出三角形的面积比较即可.
解答 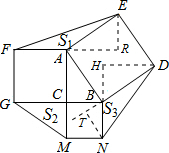 解:作ER⊥FA的延长线,垂足为R;作DH⊥NB的延长线,垂足为H;作NT垂直于DB的延长线,垂足为T.
解:作ER⊥FA的延长线,垂足为R;作DH⊥NB的延长线,垂足为H;作NT垂直于DB的延长线,垂足为T.
设△ABC的三边长分别为a、b、c,
∵分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,
∵AE=AB,∠ARE=∠ACB,∠EAR=∠CAB,
∴△AER≌△ABC,
∴ER=BC=a,
FA=b,
∴S1=$\frac{1}{2}$ab,S2=$\frac{1}{2}$ab,
同理可得HD=AR=AC,
∴S1=S2=S3=$\frac{1}{2}$ab.
故选A.
点评 本题考查的是勾股定理,三角形的面积及全等三角形的知识,解题的关键是了解三角形的三边与正方形的边长的关系.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
1. 如图,AB∥EF∥CD,∠ABC=44°,∠CEF=154°,则∠BCE等于( )
如图,AB∥EF∥CD,∠ABC=44°,∠CEF=154°,则∠BCE等于( )
 如图,AB∥EF∥CD,∠ABC=44°,∠CEF=154°,则∠BCE等于( )
如图,AB∥EF∥CD,∠ABC=44°,∠CEF=154°,则∠BCE等于( )| A. | 22° | B. | 18° | C. | 20° | D. | 26° |
8.已知|2017-a|+$\sqrt{a-2018}$=a,则a-20172的值为( )
| A. | 2017 | B. | 2018 | C. | 20172 | D. | 20182 |
15.明明家离学校1500米,其中有一段为上坡路.另一段为下坡路,某天他去学校共用了12分钟,假设明明上坡路的平均速度是5千米/时,下坡路的平均速度是8千米/时.若设明明上坡路用了x分钟,下坡路用了y分钟,根据题意可列方程组为( )
| A. | $\left\{\begin{array}{l}{x+y=12}\\{5x+8y=1500}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=12}\\{\frac{1}{12}x+\frac{2}{15}y=1.5}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{5x+8y=1.5}\\{x+y=12}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=12}\\{\frac{1}{12}x-\frac{2}{15}y=1.5}\end{array}\right.$ |
12.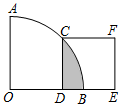 如图,在扇形OAB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,若正方形CDEF的边长为2,则图中阴影部分的面积为( )
如图,在扇形OAB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,若正方形CDEF的边长为2,则图中阴影部分的面积为( )
 如图,在扇形OAB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,若正方形CDEF的边长为2,则图中阴影部分的面积为( )
如图,在扇形OAB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,若正方形CDEF的边长为2,则图中阴影部分的面积为( )| A. | π-2 | B. | 2π-2 | C. | 4π-4 | D. | 4π-8 |
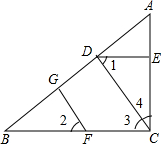 如图,已知BC⊥AC于点C,FG⊥AB于点G,∠2+∠4=90°,请说明CD⊥AB.
如图,已知BC⊥AC于点C,FG⊥AB于点G,∠2+∠4=90°,请说明CD⊥AB.