题目内容
15.明明家离学校1500米,其中有一段为上坡路.另一段为下坡路,某天他去学校共用了12分钟,假设明明上坡路的平均速度是5千米/时,下坡路的平均速度是8千米/时.若设明明上坡路用了x分钟,下坡路用了y分钟,根据题意可列方程组为( )| A. | $\left\{\begin{array}{l}{x+y=12}\\{5x+8y=1500}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=12}\\{\frac{1}{12}x+\frac{2}{15}y=1.5}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{5x+8y=1.5}\\{x+y=12}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=12}\\{\frac{1}{12}x-\frac{2}{15}y=1.5}\end{array}\right.$ |
分析 两个等量关系为:上坡用的时间+下坡用的时间=12;上坡用的时间×上坡的速度+下坡用的时间×下坡速度=1.5,把相关数值代入即可求解.
解答 解:根据题意可列方程组:$\left\{\begin{array}{l}{x+y=12}\\{\frac{x}{60}•5+\frac{y}{60}•8=1.5}\end{array}\right.$,
整理,得:$\left\{\begin{array}{l}{x+y=12}\\{\frac{1}{12}x+\frac{2}{15}y=1.5}\end{array}\right.$,
故选:B.
点评 考查用二元一次方程组解决行程问题;得到走不同路段所用时间及所走的路程之和的等量关系是解决本题的关键.解题的关键是统一单位.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
10.下列说法错误的是( )
| A. | -6是36的一个平方根 | B. | 任何正数都有两个平方根 | ||
| C. | (-8)2的平方根是8 | D. | 正数的两个平方根是一对相反数 |
20.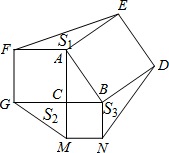 如图,△ABC中,∠ACB=90°,AC>BC,分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,连接EF、GM、ND,设△AEF、△BND、△CGM的面积分别为S1、S2、S3,则下列结论正确的是( )
如图,△ABC中,∠ACB=90°,AC>BC,分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,连接EF、GM、ND,设△AEF、△BND、△CGM的面积分别为S1、S2、S3,则下列结论正确的是( )
 如图,△ABC中,∠ACB=90°,AC>BC,分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,连接EF、GM、ND,设△AEF、△BND、△CGM的面积分别为S1、S2、S3,则下列结论正确的是( )
如图,△ABC中,∠ACB=90°,AC>BC,分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,连接EF、GM、ND,设△AEF、△BND、△CGM的面积分别为S1、S2、S3,则下列结论正确的是( )| A. | S1=S2=S3 | B. | S1=S2<S3 | C. | S1=S3<S2 | D. | S2=S3<S1 |
4.若分式$\frac{x-2}{x-3}$有意义,则x满足的条件是( )
| A. | x≠0 | B. | x≠2 | C. | x≠3 | D. | x≥3 |
5.如果a=(-π)0,b=(-0.2)-1,c=(-$\frac{1}{2}$)-2,那么a、b、c三个数的大小为( )
| A. | a>b>c | B. | c>a>b | C. | a>c>b | D. | c>b>a |