题目内容
10.【问题引入】(1)如图1,△ABC,点O是∠ABC和∠ACB相邻的外角平分线的交点,若∠A=40°,请求出∠BOC的度数.
【深入探究】
(2)如图2,在四边形ABCD中,点O是∠BAC和∠ACD的角平分线的交点,若∠B+∠D=110°,请求出∠AOC的度数.

【类比猜想】
(3)如图3,在△ABC中,∠CBO=$\frac{1}{3}$∠DBC,∠BCO=$\frac{1}{3}$∠ECB,∠A=α,则∠BOC=120°-$\frac{1}{3}$α(用α的代数式表示,直接写出结果,不需要写出解答过程).
(4)如果BO,CO分别是△ABC的外角∠DBC,∠ECB的n等分线,它们交于点O,∠CBO=$\frac{1}{n}$∠DBC,∠BCO=$\frac{1}{n}$∠ECB则∠BOC=$\frac{(n-1)×180°}{n}$-$\frac{1}{n}$α.(用n、a的代数式表示,直接写出结果,不需要写出解答过程).
分析 (1)由三角形内角和定理可求得∠ABC+∠ACB,再利用邻补角可求得∠DBC+∠ECB,根据角平分线的定义可求得∠OBC+∠OCB,在△BOC中利用三角形内角和定理可求得∠BOC;
(2)根据三角形内角和等于180°,四边形内角和等于360°,结合角平分线的定义即可得到∠AOC与∠B+∠D之间的关系;
(3)如图3,根据三角形的内角和等于180°列式整理即可得∠BOC=120°-$\frac{1}{3}$α;
(4)根据三角形的内角和等于180°列式整理即可得∠BOC=$\frac{(n-1)×180°}{n}$-$\frac{1}{n}$α.
解答 解:(1)∵∠A=40°,
∴∠ABC+∠ACB=180°-∠A=140°,
∴∠DBC+∠ECB=180°-∠ABC+180°-∠ACB=360°-(∠ABC+∠ACB)=360°-140°=220°,
∵BO、CO分别平分∠DBC和∠ECB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠DBC+∠ECB)=$\frac{1}{2}$×220°=110°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-110°=70°;
(2)∵点O是∠BAC和∠ACD的角平分线的交点,
∴∠OAC=$\frac{1}{2}$∠CAB,∠OCA=$\frac{1}{2}$∠ACD,
∴∠AOC=180°-(∠OAC+∠OCA)
=180°-$\frac{1}{2}$(∠CAB+∠ACD)
=180°-$\frac{1}{2}$(360°-∠B-∠D)
=$\frac{1}{2}$(∠B+∠D),
∵∠B+∠D=110°,
∴∠AOC=$\frac{1}{2}$(∠B+∠D)=55°;
(3)如图③,在△OBC中,∠BOC=180°-(∠OBC+∠OCB)
=180°-$\frac{1}{3}$(∠DBC+∠ECB)
=180°-$\frac{1}{3}$(∠A+∠ACB+∠A+ABC)
=180°-$\frac{1}{3}$(∠A+180°)
=120°-$\frac{1}{3}$α;
(4)在△OBC中,∠BOC=180°-(∠OBC+∠OCB)
=180°-$\frac{1}{n}$(∠DBC+∠ECB)
=180°-$\frac{1}{n}$(∠A+∠ACB+∠A+ABC)
=180°-$\frac{1}{n}$(∠A+180°)
=$\frac{(n-1)×180°}{n}$-$\frac{1}{n}$α.
故答案为:120°-$\frac{1}{3}$α;$\frac{(n-1)×180°}{n}$-$\frac{1}{n}$α.
点评 本题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.

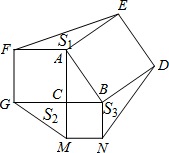 如图,△ABC中,∠ACB=90°,AC>BC,分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,连接EF、GM、ND,设△AEF、△BND、△CGM的面积分别为S1、S2、S3,则下列结论正确的是( )
如图,△ABC中,∠ACB=90°,AC>BC,分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,连接EF、GM、ND,设△AEF、△BND、△CGM的面积分别为S1、S2、S3,则下列结论正确的是( )| A. | S1=S2=S3 | B. | S1=S2<S3 | C. | S1=S3<S2 | D. | S2=S3<S1 |
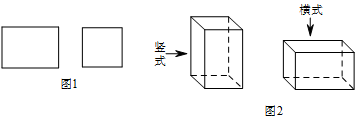
(1)若该厂购进正方形纸板1000张,长方形纸板2000张,问竖式纸盒,横式纸盒各加工多少个,恰好能将购进的纸板全部用完.
分析:思考加工一个竖式纸盒需要几张长方形和正方形纸板?加工一个横式纸盒呢?
请填写下表(设加工x只竖式纸盒,y只横式纸盒,恰好能将购进的纸板全部用完):
| x只竖式纸盒中 | y只横式纸盒中 | 合计 | |
| 正方形纸板的张数 | x | 2y | 1000 |
| 长方形纸板的张数 | 4x | 3y | 2000 |
(2)该工厂某一天使用的材料清单上显示,这天一共使用正方形纸板50张,长方形纸板a张,全部加工成上述两种纸盒,且120<a<136,试求在这一天加工两种纸盒时,a的所有可能值.
| A. | 3+$\frac{a}{3}$ | B. | 3 | C. | 4 | D. | 5 |
| A. | a>b>c | B. | c>a>b | C. | a>c>b | D. | c>b>a |
| A. | 3,4,5 | B. | 6,8,10 | C. | 1.5,2,2.5 | D. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ |
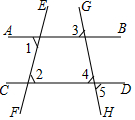 如图,已知∠1=∠2,试说明∠3=∠5.请你把说理过程补充完整.
如图,已知∠1=∠2,试说明∠3=∠5.请你把说理过程补充完整.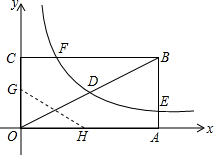 如图,矩形OABC的边长OA=8,顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过点D、E、F,且tan∠BOA=$\frac{1}{2}$.
如图,矩形OABC的边长OA=8,顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过点D、E、F,且tan∠BOA=$\frac{1}{2}$.