题目内容
12.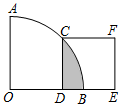 如图,在扇形OAB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,若正方形CDEF的边长为2,则图中阴影部分的面积为( )
如图,在扇形OAB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,若正方形CDEF的边长为2,则图中阴影部分的面积为( )| A. | π-2 | B. | 2π-2 | C. | 4π-4 | D. | 4π-8 |
分析 连结OC,根据勾股定理可求OC的长,根据题意可得出阴影部分的面积=扇形BOC的面积-三角形ODC的面积,依此列式计算即可求解.
解答  解:连接OC∵在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是$\widehat{AB}$的中点,
解:连接OC∵在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是$\widehat{AB}$的中点,
∴∠COD=45°,
∴OC=$\sqrt{2}$CD=2$\sqrt{2}$,
∴阴影部分的面积=扇形BOC的面积-三角形ODC的面积
=$\frac{45}{360}$×π×(2$\sqrt{2}$)2-$\frac{1}{2}$×22
=π-2.
故选:A.
点评 考查了正方形的性质和扇形面积的计算,解题的关键是得到扇形半径的长度.

练习册系列答案
相关题目
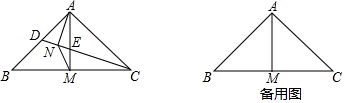
20.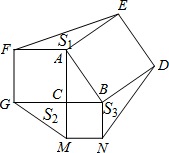 如图,△ABC中,∠ACB=90°,AC>BC,分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,连接EF、GM、ND,设△AEF、△BND、△CGM的面积分别为S1、S2、S3,则下列结论正确的是( )
如图,△ABC中,∠ACB=90°,AC>BC,分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,连接EF、GM、ND,设△AEF、△BND、△CGM的面积分别为S1、S2、S3,则下列结论正确的是( )
 如图,△ABC中,∠ACB=90°,AC>BC,分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,连接EF、GM、ND,设△AEF、△BND、△CGM的面积分别为S1、S2、S3,则下列结论正确的是( )
如图,△ABC中,∠ACB=90°,AC>BC,分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG,连接EF、GM、ND,设△AEF、△BND、△CGM的面积分别为S1、S2、S3,则下列结论正确的是( )| A. | S1=S2=S3 | B. | S1=S2<S3 | C. | S1=S3<S2 | D. | S2=S3<S1 |
4.若分式$\frac{x-2}{x-3}$有意义,则x满足的条件是( )
| A. | x≠0 | B. | x≠2 | C. | x≠3 | D. | x≥3 |
1.某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图所示的竖式与横式两种无盖的长方形纸箱.(加工时接缝材料不计)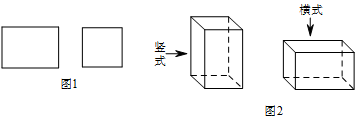
(1)若该厂购进正方形纸板1000张,长方形纸板2000张,问竖式纸盒,横式纸盒各加工多少个,恰好能将购进的纸板全部用完.
分析:思考加工一个竖式纸盒需要几张长方形和正方形纸板?加工一个横式纸盒呢?
请填写下表(设加工x只竖式纸盒,y只横式纸盒,恰好能将购进的纸板全部用完):
根据上表可得方程组$\left\{\begin{array}{l}{x+2y=1000}\\{4x+3y=2000}\end{array}\right.$;解这个方程组,得$\left\{\begin{array}{l}{x=200}\\{y=400}\end{array}\right.$.
(2)该工厂某一天使用的材料清单上显示,这天一共使用正方形纸板50张,长方形纸板a张,全部加工成上述两种纸盒,且120<a<136,试求在这一天加工两种纸盒时,a的所有可能值.

(1)若该厂购进正方形纸板1000张,长方形纸板2000张,问竖式纸盒,横式纸盒各加工多少个,恰好能将购进的纸板全部用完.
分析:思考加工一个竖式纸盒需要几张长方形和正方形纸板?加工一个横式纸盒呢?
请填写下表(设加工x只竖式纸盒,y只横式纸盒,恰好能将购进的纸板全部用完):
| x只竖式纸盒中 | y只横式纸盒中 | 合计 | |
| 正方形纸板的张数 | x | 2y | 1000 |
| 长方形纸板的张数 | 4x | 3y | 2000 |
(2)该工厂某一天使用的材料清单上显示,这天一共使用正方形纸板50张,长方形纸板a张,全部加工成上述两种纸盒,且120<a<136,试求在这一天加工两种纸盒时,a的所有可能值.
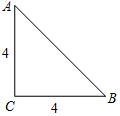 在数学活动课中,同学们准备了一些等腰直角三角形纸片,从每张纸片中剪出一个扇形制作圆锥玩具模型.如图,已知△ABC是腰长为4的等腰直角三角形.
在数学活动课中,同学们准备了一些等腰直角三角形纸片,从每张纸片中剪出一个扇形制作圆锥玩具模型.如图,已知△ABC是腰长为4的等腰直角三角形.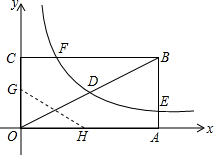 如图,矩形OABC的边长OA=8,顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过点D、E、F,且tan∠BOA=$\frac{1}{2}$.
如图,矩形OABC的边长OA=8,顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过点D、E、F,且tan∠BOA=$\frac{1}{2}$.