题目内容
已知△ABC中,∠BAC=108°,AB=AC=2,求BC的长.
考点:相似三角形的判定与性质,等腰三角形的性质
专题:
分析:在BC上截取BD=AB=2,易证AD=CD,△ABC∽△DAC,利用相似三角形的对应边的比相等即可求解.
解答: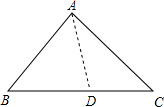 解:在BC上截取BD=AB=2.
解:在BC上截取BD=AB=2.
∵AB=AC,
∴∠B=∠C=
=72°,
又∵BD=AB,
∴∠BAD=∠ADB=
=36°,
∴∠DAC=108°-72°=36°,∠ADC=180°-36°-36°=108°,
∴AD=CD,△ABC∽△DAC,
∴
=
,
设CD=AD=x,则BC=2+x,
∴
=
,
解得:x=-1+
或-1-
(舍去).
则BC=2+(-1+
)=
+1.
 解:在BC上截取BD=AB=2.
解:在BC上截取BD=AB=2.∵AB=AC,
∴∠B=∠C=
| 180°-108° |
| 2 |
又∵BD=AB,
∴∠BAD=∠ADB=
| 180°-72° |
| 2 |
∴∠DAC=108°-72°=36°,∠ADC=180°-36°-36°=108°,
∴AD=CD,△ABC∽△DAC,
∴
| AB |
| AD |
| BC |
| AC |
设CD=AD=x,则BC=2+x,
∴
| 2 |
| x |
| 2+x |
| 2 |
解得:x=-1+
| 5 |
| 5 |
则BC=2+(-1+
| 5 |
| 5 |
点评:本题考查了相似三角形的判定与性质,正确作出辅助线是关键.

练习册系列答案
相关题目
下列图形都是由同样大小的五角星按一定的规律组成,其中第①个图形一共有2个五角星,第②个图形一共有8个五角星,第③个图形一共有18个五角星,…,则第⑦个图形中五角星的个数为( ) 

| A、84 | B、90 | C、94 | D、98 |
 如图是一块三角形的草坪,现要在草坪上建一座凉亭供大家休息,要使凉亭到草坪三条边的距离相等,则凉亭的位置应选在( )
如图是一块三角形的草坪,现要在草坪上建一座凉亭供大家休息,要使凉亭到草坪三条边的距离相等,则凉亭的位置应选在( )| A、△ABC三条中线的交点 |
| B、△ABC三边的垂直平分线的交点 |
| C、△ABC三条角平分线的交点 |
| D、△ABC三条高所在直线的交点 |
若关于x的方程
-
=1有增根,则m的值是( )
| m |
| x-1 |
| x |
| x-1 |
| A、3 | B、2 | C、1 | D、0 |
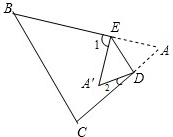 如图,把△ABC纸片沿DE折叠,点A落在四边形BCDE内部.
如图,把△ABC纸片沿DE折叠,点A落在四边形BCDE内部.