题目内容
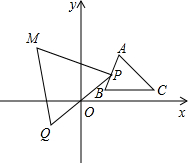如图，△ABC在第一象限，其面积为16．点P从点A出发，沿△ABC的边从A-B-C-A运动一周，在点P运动的同时，作点P关于原点O的对称点Q，再以PQ为边作等边三角形PQM，点M在第二象限，点M随点P运动所形成的图形的面积为考点：轨迹
专题：
分析：设M点对应的A，B，C的点分别为Ma，Mb，Mc，由△MbQbB是等边三角形，得出MbO=
OB，同理得出MbO=
OB，又因∠COB=∠McOMb，得出△McOMb∽△COB，得出MbMc=
BC，同理证得MaMb=
AB，MaMc=
AC，所以△MaMbMc的面积是△ABC的3倍．求出点M随点P运动所形成的图形的面积为48．
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
解答：
解：如图，
∵点P从点A出发，沿△ABC的边从A-B-C-A运动一周，且点Q关于原点O与点P对称，
∴点Q随点P运动所形成的图形是△ABC关于O的中心对称图形，
以PQ为边作等边△PQM，M点对应的A，B，C的点分别为Ma，Mb，Mc，
∵△MbQbB是等边三角形，
∴MbO=
OB，
同理McO=
OC，
∴
=
=
∵∠COB+∠BOMc=90°，∠McOMb+∠BOMc=90°
∴∠COB=∠McOMb，
∴△McOMb∽△COB，
∴MbMc=
BC，
同理，MaMb=
AB，MaMc=
AC，
∴△MaMbMc的面积=
×
×16=48，
即点M随点P运动所形成的图形的面积为48．
故答案为：48．
解：如图，
∵点P从点A出发，沿△ABC的边从A-B-C-A运动一周，且点Q关于原点O与点P对称，
∴点Q随点P运动所形成的图形是△ABC关于O的中心对称图形，
以PQ为边作等边△PQM，M点对应的A，B，C的点分别为Ma，Mb，Mc，
∵△MbQbB是等边三角形，
∴MbO=
| 3 |
同理McO=
| 3 |
∴
| MbO |
| BO |
| McO |
| CO |
| 3 |
∵∠COB+∠BOMc=90°，∠McOMb+∠BOMc=90°
∴∠COB=∠McOMb，
∴△McOMb∽△COB，
∴MbMc=
| 3 |
同理，MaMb=
| 3 |
| 3 |
∴△MaMbMc的面积=
| 3 |
| 3 |
即点M随点P运动所形成的图形的面积为48．
故答案为：48．
点评：本题主要考查了轨迹，解题的关键是找出△MaMbMc与△ABC边长的关系．
练习册系列答案
相关题目
如图是二次函数y=ax2+bx+a2-2（a、b为常数）的图象，则a=
如图，已知BO是△ABC的外接圆的半径，CD⊥AB于D．若AD=3，BD=8，CD=6，则BO的长为已知反比例函数y=-
，下列结论不正确的是（ ）
| 2 |
| x |
| A、图象必经过点（-1，2） |
| B、y随x的增大而增大 |
| C、图象分布在第二、四象限内 |
| D、若x＞1，则-2＜y＜0 |
化简：（1+
）÷
的结果为（ ）
| 1 |
| x |
| x2-1 |
| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
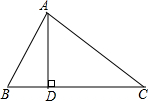在△ABC中，AD⊥BC于D，求证：AB2+CD2=AC2+BD2．