题目内容
已知关于x,y的方程组
的解为正数,则|k-6|+|k+1|= .
|
考点:二元一次方程组的解,解一元一次不等式组
专题:计算题
分析:将k看做已知数表示出x与y,根据x与y都是正数,确定出k的范围,利用绝对值的代数意义化简计算即可得到结果.
解答:解:
,
①+②得:2x=6k+4,即x=3k+2,
①-②得:2y=-2k+10,即y=-k+5,
根据题意得:
,
解得:-
<k<5,
∴k-6<0,k+1>0,
则原式=6-k+k+1=7,
故答案为:7
|
①+②得:2x=6k+4,即x=3k+2,
①-②得:2y=-2k+10,即y=-k+5,
根据题意得:
|
解得:-
| 2 |
| 3 |
∴k-6<0,k+1>0,
则原式=6-k+k+1=7,
故答案为:7
点评:此题考查了二元一次方程组的解,熟练掌握运算法则是解本题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 如图是由四个小正方体叠成的一个立体图形,那么它的左视图是( )
如图是由四个小正方体叠成的一个立体图形,那么它的左视图是( )A、 |
B、 |
C、 |
D、 |
工地上有甲、乙二块铁板,铁板甲形状为等腰三角形,其顶角为45°,腰长为12cm;铁板乙形状为直角梯形,两底边长分别为4cm、10cm,且有一内角为60°.现在我们把它们任意翻转,分别试图从一个直径为8.5cm的圆洞中穿过,结果是( )
| A、甲板能穿过,乙板不能穿过 |
| B、甲板不能穿过,乙板能穿过 |
| C、甲、乙两板都能穿过 |
| D、甲、乙两板都不能穿过 |
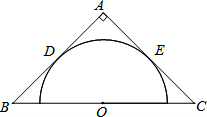 如图,在等腰直角三角形ABC中,AB=AC=8,O为BC的中点,以O为圆心作半圆,使它与AB,AC都相切,切点分别为D,E,则⊙O的半径为
如图,在等腰直角三角形ABC中,AB=AC=8,O为BC的中点,以O为圆心作半圆,使它与AB,AC都相切,切点分别为D,E,则⊙O的半径为
 小明把如图的平行四边形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是
小明把如图的平行四边形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是 如图,△ABC中,AB=AC,AD⊥BC于点D,点E在AC上,CE=2AE,AD=9,BE=10,AD与BE交于点F,则△ABC的面积是
如图,△ABC中,AB=AC,AD⊥BC于点D,点E在AC上,CE=2AE,AD=9,BE=10,AD与BE交于点F,则△ABC的面积是