题目内容
 小明把如图的平行四边形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是
小明把如图的平行四边形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是考点:几何概率,平行四边形的性质
专题:
分析:先根据平行四边形的性质求出平行四边形对角线所分的四个三角形面积相等,再求出S1=S2即可.
解答: 解:根据平行四边形的性质易证平行四边形的对角线把矩形分成的四个三角形均为同底等高的三角形,故其面积相等,
解:根据平行四边形的性质易证平行四边形的对角线把矩形分成的四个三角形均为同底等高的三角形,故其面积相等,
根据平行线的性质易证S1=S2,故阴影部分的面积占一份,
故飞镖落在阴影区域的概率为:
.
故答案为:
.
 解:根据平行四边形的性质易证平行四边形的对角线把矩形分成的四个三角形均为同底等高的三角形,故其面积相等,
解:根据平行四边形的性质易证平行四边形的对角线把矩形分成的四个三角形均为同底等高的三角形,故其面积相等,根据平行线的性质易证S1=S2,故阴影部分的面积占一份,
故飞镖落在阴影区域的概率为:
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:此题主要考查了几何概率问题,用到的知识点为:概率=相应的面积与总面积之比.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 小明仰视如图的两个物体,他看到的俯视图是( )
小明仰视如图的两个物体,他看到的俯视图是( )A、 |
B、 |
C、 |
D、 |
根据全国第六次人口普查统计,杭州市萧山区常住人口约为20330000人,近似值20330000用科学记数法可表示为( )
| A、2.033×104人 |
| B、2.033×105人 |
| C、20.33×106人 |
| D、2.033×107人 |
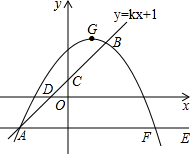 已知直线y=kx+1经过点A(d,-2)和点B(2,3),交y轴于点C,交x轴于点D.将直线AB绕点A顺时针旋转45°得到直线AE,点F(5,e)在直线AE上.经过A,B,F三点的抛物线y=ax2+bx+c的顶点为G.
已知直线y=kx+1经过点A(d,-2)和点B(2,3),交y轴于点C,交x轴于点D.将直线AB绕点A顺时针旋转45°得到直线AE,点F(5,e)在直线AE上.经过A,B,F三点的抛物线y=ax2+bx+c的顶点为G. 如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,连结AB.
如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,连结AB. 如图,圆锥的高h=4cm,底面半径r=3cm,则圆锥的全面积为
如图,圆锥的高h=4cm,底面半径r=3cm,则圆锥的全面积为 如图,由边长为1的小正方形组成的网格中,正方形ABGH,BCFG,CDEF的顶点都在网格的格点上.则tan∠BHD=
如图,由边长为1的小正方形组成的网格中,正方形ABGH,BCFG,CDEF的顶点都在网格的格点上.则tan∠BHD=