题目内容
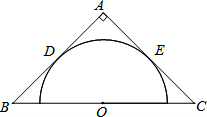 如图,在等腰直角三角形ABC中,AB=AC=8,O为BC的中点,以O为圆心作半圆,使它与AB,AC都相切,切点分别为D,E,则⊙O的半径为
如图,在等腰直角三角形ABC中,AB=AC=8,O为BC的中点,以O为圆心作半圆,使它与AB,AC都相切,切点分别为D,E,则⊙O的半径为考点:切线的性质,等腰直角三角形
专题:
分析:连接OD、OE,可证明四边形ODAE为正方形,再根据O为BC的中点,可得出OD为△ABC的中位线,从而得出⊙O的半径为4.
解答: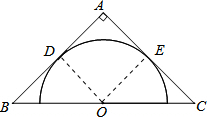 解:连接OD、OE,
解:连接OD、OE,
∵AB,AC为⊙O的切线,
∴OD⊥AB,OE⊥AC,
∴∠=∠=90°,
∵∠A=90°
∴四边形ODAE为矩形,
∵OD=OE,
∴四边形ODAE为正方形,
∵O为BC的中点,
∴OD为△ABC的中位线,
∵AB=AC=8,
∵OD=4,
∴⊙O的半径为4.
故答案为4.
 解:连接OD、OE,
解:连接OD、OE,∵AB,AC为⊙O的切线,
∴OD⊥AB,OE⊥AC,
∴∠=∠=90°,
∵∠A=90°
∴四边形ODAE为矩形,
∵OD=OE,
∴四边形ODAE为正方形,
∵O为BC的中点,
∴OD为△ABC的中位线,
∵AB=AC=8,
∵OD=4,
∴⊙O的半径为4.
故答案为4.
点评:本题考查了切线的性质、三角形中位线的判定以及等腰直角三角形的性质,经过三角形一边的中点,平行于另一边的直线,必平分第三边.

练习册系列答案
相关题目
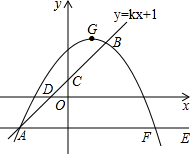 已知直线y=kx+1经过点A(d,-2)和点B(2,3),交y轴于点C,交x轴于点D.将直线AB绕点A顺时针旋转45°得到直线AE,点F(5,e)在直线AE上.经过A,B,F三点的抛物线y=ax2+bx+c的顶点为G.
已知直线y=kx+1经过点A(d,-2)和点B(2,3),交y轴于点C,交x轴于点D.将直线AB绕点A顺时针旋转45°得到直线AE,点F(5,e)在直线AE上.经过A,B,F三点的抛物线y=ax2+bx+c的顶点为G.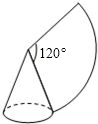 如图,用圆心角为120°半径为6的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的高是
如图,用圆心角为120°半径为6的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的高是 如图,⊙M的圆心在x轴上,⊙M与坐标轴的交点A、B坐标分别是A(0,4),B(8,0),则点M坐标为
如图,⊙M的圆心在x轴上,⊙M与坐标轴的交点A、B坐标分别是A(0,4),B(8,0),则点M坐标为 如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,连结AB.
如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,连结AB.