题目内容
今有一副三角板(如图1),中间各有一个直径为6cm的圆洞,现将三角形a的30°角的那一头插入三角板b的圆洞内(如图2),则三角板a通过三角板b的圆洞的那一部分的最大面积为 cm2(不计三角板的厚度,精确到0.1cm2).


考点:解直角三角形的应用
专题:
分析:作AD⊥BC,当点D是BC的中点时,△ABC的面积最大,此时由中垂线的性质知,AB=AC,∠B=75°,可求S△ABC=
BC•BDtan75°.
| 1 |
| 2 |
解答:解:如图,BC=6cm,∠BAC=30°,
作AD⊥BC于点D,
当点D是BC的中点时,△ABC的面积最大,
此时由中垂线的性质知,AB=AC,∠B=75°,
S△ABC=
BC•BDtan75°=
×6×3×3.732≈33.6(cm2).
故答案为:33.6.

作AD⊥BC于点D,
当点D是BC的中点时,△ABC的面积最大,
此时由中垂线的性质知,AB=AC,∠B=75°,
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:33.6.
点评:本题考查了解直角三角形的应用,利用了中垂线的性质,三角形的面积公式,正切的概念求解.

练习册系列答案
相关题目
若分式
的值为0,则x的值是( )
| x2-9 |
| (x+3)2 |
| A、x=0 | B、x=-3 |
| C、x=±3 | D、x=3 |
 如图,⊙M的圆心在x轴上,⊙M与坐标轴的交点A、B坐标分别是A(0,4),B(8,0),则点M坐标为
如图,⊙M的圆心在x轴上,⊙M与坐标轴的交点A、B坐标分别是A(0,4),B(8,0),则点M坐标为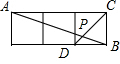 如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,连结AB.
如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,连结AB. 如图,圆锥的高h=4cm,底面半径r=3cm,则圆锥的全面积为
如图,圆锥的高h=4cm,底面半径r=3cm,则圆锥的全面积为