题目内容
14.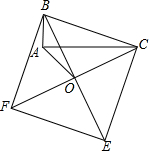 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.如果AB=2,AO=2$\sqrt{2}$,那么AC的长等于( )
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.如果AB=2,AO=2$\sqrt{2}$,那么AC的长等于( )| A. | 4 | B. | 6 | C. | 4$\sqrt{2}$ | D. | 6$\sqrt{2}$ |
分析 在AC上截取CG=AB=2,连接OG,根据B、A、O、C四点共圆,推出∠ABO=∠ACO,证△BAO≌△CGO,推出OA=OG=2,∠AOB=∠COG,得出等腰直角三角形AOG,根据勾股定理求出AG,即可求出AC.
解答  解:在AC上截取CG=AB=2,连接OG,
解:在AC上截取CG=AB=2,连接OG,
∵四边形BCEF是正方形,∠BAC=90°,
∴OB=OC,∠BAC=∠BOC=90°,
∴B、A、O、C四点共圆,
∴∠ABO=∠ACO,
在△BAO和△CGO中
$\left\{\begin{array}{l}{BA=CG}\\{∠BAO=∠GCO}\\{OB=OC}\end{array}\right.$,
∴△BAO≌△CGO(SAS),
∴OA=OG=2$\sqrt{2}$,∠AOB=∠COG,
∵∠BOC=∠COG+∠BOG=90°,
∴∠AOG=∠AOB+∠BOG=90°,
即△AOG是等腰直角三角形,
由勾股定理得:AG=$\sqrt{{AO}^{2}{+OG}^{2}}$=4,
即AC=4+2=6,
故选B.
点评 本题主要考查了勾股定理,正方形的性质,直角三角形的性质,全等三角形的性质和判定等知识点的理解和掌握,能熟练地运用这些性质进行推理和计算是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.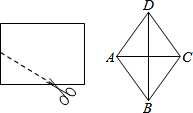 如图,将一个长为10,宽为8的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )
如图,将一个长为10,宽为8的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )
 如图,将一个长为10,宽为8的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )
如图,将一个长为10,宽为8的矩形纸片对折两次后,沿所得矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )| A. | 10 | B. | 20 | C. | 40 | D. | 80 |
2. 如图,有一把折扇和一把团扇,已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120°.问哪一把扇子扇面的面积大( )
如图,有一把折扇和一把团扇,已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120°.问哪一把扇子扇面的面积大( )
 如图,有一把折扇和一把团扇,已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120°.问哪一把扇子扇面的面积大( )
如图,有一把折扇和一把团扇,已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120°.问哪一把扇子扇面的面积大( )| A. | 折扇大 | B. | 团扇大 | C. | 一样大 | D. | 不能比较 |
19.方程$2{x^2}-3x=\frac{1}{2}({{x^2}-6x})$的解是( )
| A. | 0,0 | B. | 0,3 | C. | 0,2 | D. | 0,$\frac{1}{3}$ |
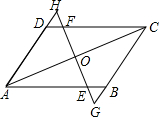 如图,已知AD∥BC,AD=BC,O为AC的中点,过点O作直线交AB于点E,交DC于F,交AD的延长线于H,交CB的延长线于G.
如图,已知AD∥BC,AD=BC,O为AC的中点,过点O作直线交AB于点E,交DC于F,交AD的延长线于H,交CB的延长线于G.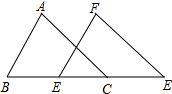 如图,B、C、D、E在同一直线上,已知AB∥FC,AB=FC,BC=DE,求证:AD${\;}_{=}^{∥}$FE.
如图,B、C、D、E在同一直线上,已知AB∥FC,AB=FC,BC=DE,求证:AD${\;}_{=}^{∥}$FE. 如图,已知BC是⊙O的直径,AB是⊙O的弦,OD⊥AB于点P,交劣弧AB于点D.
如图,已知BC是⊙O的直径,AB是⊙O的弦,OD⊥AB于点P,交劣弧AB于点D.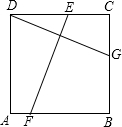 如图,E,F,G是正方形ABCD的边DC,AB,BC上的点,点D与点G关于EF对称,若DG=9cm,则EF=9cm.
如图,E,F,G是正方形ABCD的边DC,AB,BC上的点,点D与点G关于EF对称,若DG=9cm,则EF=9cm.