题目内容
9.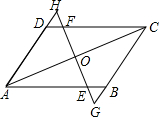 如图,已知AD∥BC,AD=BC,O为AC的中点,过点O作直线交AB于点E,交DC于F,交AD的延长线于H,交CB的延长线于G.
如图,已知AD∥BC,AD=BC,O为AC的中点,过点O作直线交AB于点E,交DC于F,交AD的延长线于H,交CB的延长线于G.(1)说明:OH=OG;
(2)说明:△GBE≌△HDF.
分析 (1)由题中条件及平行四边形的性质不难得出△ODH≌△OBG,进而可得出结论;
(2)由(1)证得△ODH≌△OBG,得到DH=BG,根据AB∥CD,得到∠DFO=∠OEB,由邻补角的性质得到∠DFH=∠EBG,即可证得结论.
解答 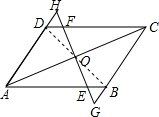 证明:(1)连接BD,
证明:(1)连接BD,
∵四边形ABCD是平行四边形,O为AC的中点,
∴OB=OD.
∵AD∥BC,∴∠H=∠G.
在△DOH与△OBG中,$\left\{\begin{array}{l}{∠DOH=∠BOG}\\{∠H=∠G}\\{OD=OB}\end{array}\right.$'
∴△ODH≌△OBG,
∴OH=OG;
(2)由(1)证得△ODH≌△OBG,
∴DH=BG,
∵AB∥CD,
∴∠DFO=∠OEB,
∴∠DFH=∠EBG,
在△DHF与△BEG中,$\left\{\begin{array}{l}{∠H=∠G}\\{DH=BG}\\{∠HDF=∠EBG}\end{array}\right.$,
∴△GBE≌△HDF.
点评 本题主要考查平行四边形的性质及全等三角形的判定及性质,能够熟练掌握判定定理是解题的关键.

练习册系列答案
相关题目
14.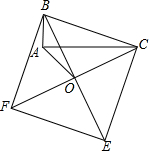 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.如果AB=2,AO=2$\sqrt{2}$,那么AC的长等于( )
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.如果AB=2,AO=2$\sqrt{2}$,那么AC的长等于( )
 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.如果AB=2,AO=2$\sqrt{2}$,那么AC的长等于( )
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.如果AB=2,AO=2$\sqrt{2}$,那么AC的长等于( )| A. | 4 | B. | 6 | C. | 4$\sqrt{2}$ | D. | 6$\sqrt{2}$ |
1.若方程x2-nx+n+2=0的两根平方和等于4,则n的值是( )
| A. | 2或-4 | B. | -2或4 | C. | 2或4 | D. | -2 |
18.有3个完全相同的小球,把它们分别标号为1,2,3,放在一个不透明的口袋中,随机地摸出一个小球不放回,再随机地摸出一个小球,则摸出的两个球号码之和等于3的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
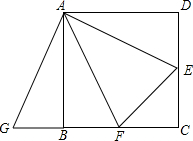 已知:如图,在正方形ABCD中,AD=AB,∠D=∠ABC=90°,∠BAD=90°,E,F分别CD,BC边上的点,且∠EAF=45°,延长CB到点G,使BG=DE,连接EF,AG.求证:
已知:如图,在正方形ABCD中,AD=AB,∠D=∠ABC=90°,∠BAD=90°,E,F分别CD,BC边上的点,且∠EAF=45°,延长CB到点G,使BG=DE,连接EF,AG.求证: