题目内容
6.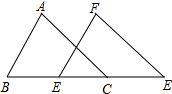 如图,B、C、D、E在同一直线上,已知AB∥FC,AB=FC,BC=DE,求证:AD${\;}_{=}^{∥}$FE.
如图,B、C、D、E在同一直线上,已知AB∥FC,AB=FC,BC=DE,求证:AD${\;}_{=}^{∥}$FE.
分析 首先得出BD=CE,利用平行线的性质∠B=∠FCE,再利用AAS得出△ABC≌△DEF,即可得出答案.
解答 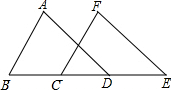 证明;∵BC=DE,
证明;∵BC=DE,
∴BC+CD=DE+CD,
即:BD=CE,
∵AB∥FC,
∴∠B=∠FCE,
在△ABD与△FCE中,
$\left\{\begin{array}{l}{AB=CF}\\{∠B=∠FCE}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△FCE,
∴AD=FE,∠ADB=∠E,
∴AD∥FE.
点评 此题主要考查了平行线的性质以及全等三角形的判定与性质,熟练掌握全等三角形的判定方法是解题关键.

练习册系列答案
相关题目
14.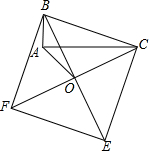 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.如果AB=2,AO=2$\sqrt{2}$,那么AC的长等于( )
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.如果AB=2,AO=2$\sqrt{2}$,那么AC的长等于( )
 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.如果AB=2,AO=2$\sqrt{2}$,那么AC的长等于( )
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.如果AB=2,AO=2$\sqrt{2}$,那么AC的长等于( )| A. | 4 | B. | 6 | C. | 4$\sqrt{2}$ | D. | 6$\sqrt{2}$ |
1.若方程x2-nx+n+2=0的两根平方和等于4,则n的值是( )
| A. | 2或-4 | B. | -2或4 | C. | 2或4 | D. | -2 |
18.有3个完全相同的小球,把它们分别标号为1,2,3,放在一个不透明的口袋中,随机地摸出一个小球不放回,再随机地摸出一个小球,则摸出的两个球号码之和等于3的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
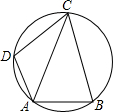 如图,在圆的内接四边形ABCD中,对角线AC平分∠DAB,若∠DAB=120°,AD=1,AC=3.4,求线段AB的长.
如图,在圆的内接四边形ABCD中,对角线AC平分∠DAB,若∠DAB=120°,AD=1,AC=3.4,求线段AB的长.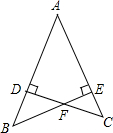 已知CD⊥AB,BE⊥AC,AB=AC,求证:DF=EF.
已知CD⊥AB,BE⊥AC,AB=AC,求证:DF=EF.