题目内容
4.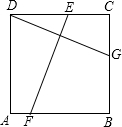 如图,E,F,G是正方形ABCD的边DC,AB,BC上的点,点D与点G关于EF对称,若DG=9cm,则EF=9cm.
如图,E,F,G是正方形ABCD的边DC,AB,BC上的点,点D与点G关于EF对称,若DG=9cm,则EF=9cm.
分析 作EM⊥AB于M,则∠EMF=90°,EM=BC,由正方形的性质得出∠C=90°,BC=DC,DC∥AB,再证出∠EFM=∠DGC,由AAS证明△EFM≌△DGC,得出对应边相等即可.
解答 解:作EM⊥AB于M,如图所示: 则∠EMF=90°,EM=BC,
则∠EMF=90°,EM=BC,
∵四边形ABCD是正方形,
∴∠C=90°,BC=DC,DC∥AB,
∴∠CDG+∠DGC=90°,∠DEN=∠EFM,EM=DC,
∵点D与点G关于EF对称,
∴EF垂直平分DG,
∴∠DNE=90°,
∴∠CDG+∠DEN=90°,
∴∠DGC=∠DEN,
∴∠EFM=∠DGC,
在△EFM和△DGC中,
$\left\{\begin{array}{l}{∠EMF=∠C=90°}&{\;}\\{∠EFM=∠DGC}&{\;}\\{EM=DC}&{\;}\end{array}\right.$,
∴△EFM≌△DGC(AAS),
∴EF=DG=9cm.
故答案为:9.
点评 本题考查了正方形的性质、轴对称的性质、全等三角形的判定与性质;熟练掌握正方形和轴对称的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
14.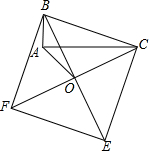 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.如果AB=2,AO=2$\sqrt{2}$,那么AC的长等于( )
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.如果AB=2,AO=2$\sqrt{2}$,那么AC的长等于( )
 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.如果AB=2,AO=2$\sqrt{2}$,那么AC的长等于( )
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.如果AB=2,AO=2$\sqrt{2}$,那么AC的长等于( )| A. | 4 | B. | 6 | C. | 4$\sqrt{2}$ | D. | 6$\sqrt{2}$ |
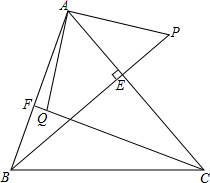 如图,已知BE是△ABC的高,点F是AB上一点,点P为BE延长线上的一点,点Q为CF上的一点,△PAB≌△AQC,则AP与AQ有怎样的关系?请说明理由.
如图,已知BE是△ABC的高,点F是AB上一点,点P为BE延长线上的一点,点Q为CF上的一点,△PAB≌△AQC,则AP与AQ有怎样的关系?请说明理由.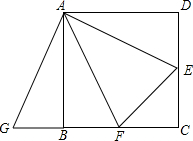 已知:如图,在正方形ABCD中,AD=AB,∠D=∠ABC=90°,∠BAD=90°,E,F分别CD,BC边上的点,且∠EAF=45°,延长CB到点G,使BG=DE,连接EF,AG.求证:
已知:如图,在正方形ABCD中,AD=AB,∠D=∠ABC=90°,∠BAD=90°,E,F分别CD,BC边上的点,且∠EAF=45°,延长CB到点G,使BG=DE,连接EF,AG.求证: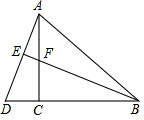 如图,在△ABC中,AC=BC,∠ACB=90°,延长BC到D,使BD=BA,BE⊥AD于点E,交AC于点F.
如图,在△ABC中,AC=BC,∠ACB=90°,延长BC到D,使BD=BA,BE⊥AD于点E,交AC于点F.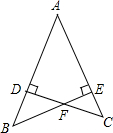 已知CD⊥AB,BE⊥AC,AB=AC,求证:DF=EF.
已知CD⊥AB,BE⊥AC,AB=AC,求证:DF=EF.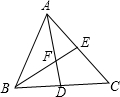 如图,△ABC的中线AD、BE相交于点F,若△ABF的面积为1,则四边形FDCE的面积是1.
如图,△ABC的中线AD、BE相交于点F,若△ABF的面积为1,则四边形FDCE的面积是1.