题目内容
3. 如图,已知BC是⊙O的直径,AB是⊙O的弦,OD⊥AB于点P,交劣弧AB于点D.
如图,已知BC是⊙O的直径,AB是⊙O的弦,OD⊥AB于点P,交劣弧AB于点D.(1)请写出三个不同的正确结论;
(2)若AB=8,DP=2,求⊙O的半径.
分析 (1)先根据垂径定理有PA=PB,又BC是直径,那么∠CAB=90°,而∠OPB=90°,那么∠CAB=∠OPB,利用同位角相等两直线平行可知OD∥AC.
(2)根据AB是⊙O的直径,BC是弦,OD⊥AB于P,得出PA=BP,设半径为R,则BP=4,OP=R-2,得到R2=(R-2)2+42,再解方程即可.
解答 解:(1)结论:PA=PB,∠CAB=90°,AC∥OD.
证明:∵OD⊥AB,OD是半径,
∴PA=PB,
∵BC是直径,
∴∠CAB=90°,
又∵OD⊥AB,
∴∠CAB=90°,
∴∠CAB=∠OPB,
∴OD∥AC.
(2)∵BC是⊙O的直径,AB是弦,OD⊥AB于点P,
∴OD垂直平分AB,
∵AB=8,DP=2
设半径为R,则PB=4,OP=R-2,
∴R2=(R-2)2+42
∴R=5.
∴⊙O的半径是5.
点评 本题考查了垂径定理、直径所对的圆周角等于90°、平行线的判定、勾股定理,解题的关键是正确地构造直角三角形.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
13.下列计算正确的是( )
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | $\sqrt{{2^2}+{3^2}}=2+3$ | C. | $\sqrt{{{(-3)}^2}}=-3$ | D. | $\sqrt{3}•\sqrt{2}=\sqrt{6}$ |
14.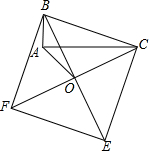 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.如果AB=2,AO=2$\sqrt{2}$,那么AC的长等于( )
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.如果AB=2,AO=2$\sqrt{2}$,那么AC的长等于( )
 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.如果AB=2,AO=2$\sqrt{2}$,那么AC的长等于( )
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.如果AB=2,AO=2$\sqrt{2}$,那么AC的长等于( )| A. | 4 | B. | 6 | C. | 4$\sqrt{2}$ | D. | 6$\sqrt{2}$ |
18.有3个完全相同的小球,把它们分别标号为1,2,3,放在一个不透明的口袋中,随机地摸出一个小球不放回,再随机地摸出一个小球,则摸出的两个球号码之和等于3的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
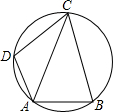 如图,在圆的内接四边形ABCD中,对角线AC平分∠DAB,若∠DAB=120°,AD=1,AC=3.4,求线段AB的长.
如图,在圆的内接四边形ABCD中,对角线AC平分∠DAB,若∠DAB=120°,AD=1,AC=3.4,求线段AB的长.
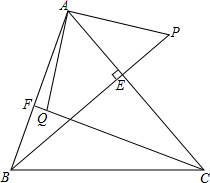 如图,已知BE是△ABC的高,点F是AB上一点,点P为BE延长线上的一点,点Q为CF上的一点,△PAB≌△AQC,则AP与AQ有怎样的关系?请说明理由.
如图,已知BE是△ABC的高,点F是AB上一点,点P为BE延长线上的一点,点Q为CF上的一点,△PAB≌△AQC,则AP与AQ有怎样的关系?请说明理由.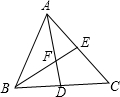 如图,△ABC的中线AD、BE相交于点F,若△ABF的面积为1,则四边形FDCE的面积是1.
如图,△ABC的中线AD、BE相交于点F,若△ABF的面积为1,则四边形FDCE的面积是1.