题目内容
2. 如图,有一把折扇和一把团扇,已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120°.问哪一把扇子扇面的面积大( )
如图,有一把折扇和一把团扇,已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120°.问哪一把扇子扇面的面积大( )| A. | 折扇大 | B. | 团扇大 | C. | 一样大 | D. | 不能比较 |
分析 折扇扇面的面积等于两个扇形的面积之差,利用扇形的面积公式:S=$\frac{n{πR}^{2}}{360}$即可得到折扇的面积,而团扇的面积即为圆的面积,然后比较它们的面积大小即可判断.
解答 解:∵折扇的面积=$\frac{120π×[{a}^{2}-(\frac{1}{2}a)^{2}]}{360}$=$\frac{π}{4}$a2,
团扇的面积=π×($\frac{a}{2}$)2=π×$\frac{1}{4}$a2=$\frac{π}{4}$a2,
∴折扇的面积=团扇的面积.
故选C.
点评 本题考查的是扇形面积的计算,熟记扇形的面积公式即可得出结论.

练习册系列答案
相关题目
12.若(m-2)x|m-3|=4是一元一次方程,则m的值是( )
| A. | 4或2 | B. | 2 | C. | 4 | D. | -4 |
13.下列计算正确的是( )
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | $\sqrt{{2^2}+{3^2}}=2+3$ | C. | $\sqrt{{{(-3)}^2}}=-3$ | D. | $\sqrt{3}•\sqrt{2}=\sqrt{6}$ |
14.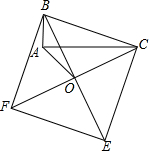 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.如果AB=2,AO=2$\sqrt{2}$,那么AC的长等于( )
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.如果AB=2,AO=2$\sqrt{2}$,那么AC的长等于( )
 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.如果AB=2,AO=2$\sqrt{2}$,那么AC的长等于( )
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO.如果AB=2,AO=2$\sqrt{2}$,那么AC的长等于( )| A. | 4 | B. | 6 | C. | 4$\sqrt{2}$ | D. | 6$\sqrt{2}$ |
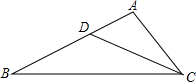 如图所示,点D是△ABC的AB边上一点,且AD=1,BD=2,AC=$\sqrt{3}$.求证:△ACD∽△ABC.
如图所示,点D是△ABC的AB边上一点,且AD=1,BD=2,AC=$\sqrt{3}$.求证:△ACD∽△ABC.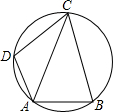 如图,在圆的内接四边形ABCD中,对角线AC平分∠DAB,若∠DAB=120°,AD=1,AC=3.4,求线段AB的长.
如图,在圆的内接四边形ABCD中,对角线AC平分∠DAB,若∠DAB=120°,AD=1,AC=3.4,求线段AB的长.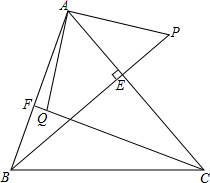 如图,已知BE是△ABC的高,点F是AB上一点,点P为BE延长线上的一点,点Q为CF上的一点,△PAB≌△AQC,则AP与AQ有怎样的关系?请说明理由.
如图,已知BE是△ABC的高,点F是AB上一点,点P为BE延长线上的一点,点Q为CF上的一点,△PAB≌△AQC,则AP与AQ有怎样的关系?请说明理由.