题目内容
13．已知P（-3，5），Q（-6，-7）在y轴上有动点M，求△PQM最小时M的坐标，并求出PM+OM的最小值．分析 画出直角坐标系，描出M、N两点，再作出M关于y轴的对称点M′，连接NM′，与y轴相交于点P，则P点即为所求，用待定系数法求出过NM′两点直线的解析式，再求出直线与y轴的交点即为P点的坐标；
解答 
解：如图所示，作出P关于y轴的对称点P′，连接P′Q，与y轴相交于点M，则M点即为所求，此时PM+QM的值最小，最小值为P′Q，因为PQ为定值，所以△PQM最小．
作QN垂直PP′的延长线于N，则QN=5+7=12，PN=3+6=9，
∴P′Q=$\sqrt{1{2}^{2}+{9}^{2}}$=15．
∴PM+QM的最小值为15．
点评 本题考查的是最短路线问题及勾股定理的应用，熟练掌握轴对称的性质和勾股定理是解题的关键．
练习册系列答案
相关题目
3．下列等式成立的是（ ）
| A． | 2-2=-22 | B． | 26÷23=22 | C． | （23）2=25 | D． | 20=1 |
4．甲、乙两班参加市统考，两班的平均分和方差分别为$\overline{{X}_{甲}}$=86分，$\overline{{X}_{乙}}$=86分，S甲2=263，S乙2=236，那么成绩较为整齐的是（ ）
| A． | 甲班 | B． | 乙班 | C． | 两班一样整齐 | D． | 无法确定 |
1．
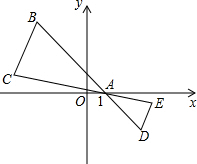如图，在△ABC中，B，C两个顶点在x轴的上方，点A的坐标是（1，0），以点A为位似图形，并把△ABC的边长缩小为原来的$\frac{1}{2}$倍，记所得的位似图形为△ADE．设点C的对应点E的横坐标为a，则点C的横坐标为（ ）
如图，在△ABC中，B，C两个顶点在x轴的上方，点A的坐标是（1，0），以点A为位似图形，并把△ABC的边长缩小为原来的$\frac{1}{2}$倍，记所得的位似图形为△ADE．设点C的对应点E的横坐标为a，则点C的横坐标为（ ）| A． | $\frac{1}{2}$（a-1） | B． | $\frac{1}{2}$（a+1） | C． | 3-2a | D． | 2（a-1） |
如图，为测量某建筑物BC及上面旗杆AB的高度，小明在距建筑物BC底部12m的点F处，测得视线点E与旗杆AB的顶端A的仰角为52°，测得视线点E与旗杆AB的底端B是仰角为45°，已知小明的身高EF为1.6m．
如图，EF⊥BC，DE⊥AB，∠B=∠ADE=30°．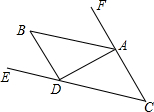
如图，已知AB∥CD，AB是∠FAD的平分线，∠C=45°．