Question

1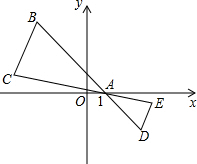．如图，在△ABC中，B，C两个顶点在x轴的上方，点A的坐标是（1，0），以点A为位似图形，并把△ABC的边长缩小为原来的$\frac{1}{2}$倍，记所得的位似图形为△ADE．设点C的对应点E的横坐标为a，则点C的横坐标为（　　）

• A． $\frac{1}{2}$（a-1）
• B． $\frac{1}{2}$（a+1）
• C． 3-2a
• D． 2（a-1）

Answer 1

分析 利用位似图形的性质得出AN，AM的长，进而得出C点横坐标．

解答 解：过点C作CN⊥x轴于点N，过点E作EM⊥x轴于点M，
∵点A的坐标是（1，0），以点A为位似图形，
并把△ABC的边长缩小为原来的$\frac{1}{2}$倍，记所得的位似图形为△ADE，点C的对应点E的横坐标为a，
∴AM=a-1，AN=2a-2，
则点C的横坐标为：-（2a-2-1）=-2a+3．
故选：C．

点评 此题主要考查了位似变换，根据题意得出对应线段的长是解题关键．