题目内容
8. 如图,为测量某建筑物BC及上面旗杆AB的高度,小明在距建筑物BC底部12m的点F处,测得视线点E与旗杆AB的顶端A的仰角为52°,测得视线点E与旗杆AB的底端B是仰角为45°,已知小明的身高EF为1.6m.
如图,为测量某建筑物BC及上面旗杆AB的高度,小明在距建筑物BC底部12m的点F处,测得视线点E与旗杆AB的顶端A的仰角为52°,测得视线点E与旗杆AB的底端B是仰角为45°,已知小明的身高EF为1.6m.(1)求建筑物BC的高度;
(2)求旗杆AB的高度(结果精确到0.1m).
(参考数据:sin52°=0.79,cos52°=0.62,tan52°=1.28)
分析 (1)先过点E作ED⊥BC于D,由视线点E与旗杆AB的底端B的仰角为45°得BD=ED=FC=12,DC=EF=1.6,从而求出BC;
(2)由已知由视线点E与旗杆AB的顶端A的仰角52°可求出AD,则AB=AD-BD.
解答 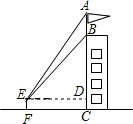 解:(1)过点E作ED⊥AC于点D,则四边形DCFE为矩形.
解:(1)过点E作ED⊥AC于点D,则四边形DCFE为矩形.
∴∠ADE=90°,CD=EF=1.6,ED=FC=12.
在Rt△BED中,∵DE=12,∠BED=45°,
∴BD=ED•tan∠BED=12×tan45°=12.
∴BC=BD+CD=12+1.6=13.6(m).
答:建筑物BC的高度为13.6m;
(2)在Rt△AED中,∵DE=12,∠AED=52°,
∴AD=ED•tan∠AED=12×tan52°=15.36.
∴AB=AD-BD=15.36-12=3.36≈3.4(m).
答:旗杆AB的高度约为3.4m.
点评 此题考查的知识点是解直角三角形的应用,解题的关键是把实际问题转化为解直角三角形问题,先得到等腰直角三角形,再根据三角函数求解.

练习册系列答案
相关题目
17. 如图,在平面直角坐标系中,点P(m,n)是动点,且m、n的关系满足下表:
如图,在平面直角坐标系中,点P(m,n)是动点,且m、n的关系满足下表:
(1)①写出m、n的关系式n=-m+1;②再写出一组满足关系的m、n的值4,-3;
(2)将每一直列中m的值作为点的横坐标,n的值作为点的纵坐标,在同一平面直角坐标系中分别描出这些点,并用线顺次连接这些点,观察它是一个什么图形?
 如图,在平面直角坐标系中,点P(m,n)是动点,且m、n的关系满足下表:
如图,在平面直角坐标系中,点P(m,n)是动点,且m、n的关系满足下表:| m | … | -3 | -2 | 0 | 1 | 2 | 3 | … |
| n | … | 4 | 3 | 1 | 0 | -1 | -2 | … |
(2)将每一直列中m的值作为点的横坐标,n的值作为点的纵坐标,在同一平面直角坐标系中分别描出这些点,并用线顺次连接这些点,观察它是一个什么图形?
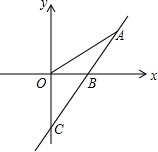 如图,直线y=kx-4与x轴,y轴分别交于B、C两点.且tan∠OBC=$\frac{4}{3}$.
如图,直线y=kx-4与x轴,y轴分别交于B、C两点.且tan∠OBC=$\frac{4}{3}$. 如图,AB∥CD,∠A=40°,∠E=25°,则∠C等于65°.
如图,AB∥CD,∠A=40°,∠E=25°,则∠C等于65°.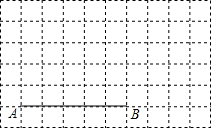 如图,在10×6的正方形网络中,每一个小正方形的边长均为1,线段AB的端点A、B均为在小正方形的顶点上.
如图,在10×6的正方形网络中,每一个小正方形的边长均为1,线段AB的端点A、B均为在小正方形的顶点上.