题目内容
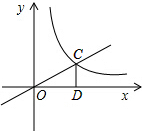 如图,已知正比例函数y=kx(k≠0)的图象与反比例函数y=
如图,已知正比例函数y=kx(k≠0)的图象与反比例函数y=| m |
| x |
| 2 |
(1)求正比例函数和反比例函数的解析式.
(2)在第一象限的反比例函数图象上求出点P,使S△ODP=2S△ODC.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)根据条件可求出C点坐标,代入两函数解析式可求得k和m的值,求得解析式;
(2)设出P点坐标,表示出△ODP和△ODC的面积得到关于P点坐标的方程求解即可.
(2)设出P点坐标,表示出△ODP和△ODC的面积得到关于P点坐标的方程求解即可.
解答:解:
(1)∵CD=OD,CD⊥x轴,
∴OC=
OD=
,
∴OD=CD=1,
∴C点坐标为(1,1),
∵两函数图象的交点为C,
∴k=1,m=1,
∴正比例函数解析式为y=x,反比例函数解析式为y=
;
(2)由(1)可知OD=CD=1,
∴S△ODC=
OD•OC=
×1×1=
,
设P点坐标为(x,
)(x>0),则S△ODP=
×1×
=
,
当S△ODP=2S△ODC时,则有
=2×
,
解得x=
,
∴P点坐标为(
,2).
(1)∵CD=OD,CD⊥x轴,
∴OC=
| 2 |
| 2 |
∴OD=CD=1,
∴C点坐标为(1,1),
∵两函数图象的交点为C,
∴k=1,m=1,
∴正比例函数解析式为y=x,反比例函数解析式为y=
| 1 |
| x |
(2)由(1)可知OD=CD=1,
∴S△ODC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
设P点坐标为(x,
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| 2x |
当S△ODP=2S△ODC时,则有
| 1 |
| 2x |
| 1 |
| 2 |
解得x=
| 1 |
| 2 |
∴P点坐标为(
| 1 |
| 2 |
点评:本题主要考查函数交点,掌握图象的交点坐标满足每个函数解析式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图是用两种正多边形密铺的平面图形图案中的一部分,其中一种是正方形,另一种与正方形相邻的四个正多边形是全等图形,那么这种正多边形是( )
如图是用两种正多边形密铺的平面图形图案中的一部分,其中一种是正方形,另一种与正方形相邻的四个正多边形是全等图形,那么这种正多边形是( )| A、正五边形、轴对称图形 |
| B、正六边形、中心对称图形 |
| C、正七边形、轴对称图形 |
| D、正八边形、中心对称图形 |
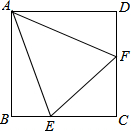 如图,在正方形ABCD中,∠EAF=45°,BE=2,DF=6,则EF的长是
如图,在正方形ABCD中,∠EAF=45°,BE=2,DF=6,则EF的长是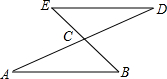 如图,AC=DC,BC=EC,求证:DE∥AB.
如图,AC=DC,BC=EC,求证:DE∥AB.