题目内容
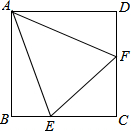 如图,在正方形ABCD中,∠EAF=45°,BE=2,DF=6,则EF的长是
如图,在正方形ABCD中,∠EAF=45°,BE=2,DF=6,则EF的长是考点:旋转的性质,全等三角形的判定与性质,勾股定理
专题:
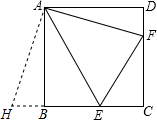
分析:延长EB至H,使BH=DF,连接AH,证△ADF≌△ABH,△FAE≌△HAE,根据全等三角形的性质得出EF=HE=BE+HB进而求出即可.
解答:解:延长EB至H,使BH=DF,连接AH,
∵在正方形ABCD中,
∴∠ADF=∠ABH,AD=AB,
在△ADF和△ABH中,
,
∴△ADF≌△ABH(SAS),
∴∠BAH=∠DAF,AF=AH,
∴∠FAH=90°,
∴∠EAF=∠EAH=45°,
在△FAE和△HAE中,
,
∴△FAE≌△HAE(SAS),
∴EF=HE=BE+HB,
∴EF=BE+DF,
∵BE=2,DF=6,
∴EF=2+6=8.
故答案为:8.
∵在正方形ABCD中,
∴∠ADF=∠ABH,AD=AB,
在△ADF和△ABH中,
|

∴△ADF≌△ABH(SAS),
∴∠BAH=∠DAF,AF=AH,
∴∠FAH=90°,
∴∠EAF=∠EAH=45°,
在△FAE和△HAE中,
|
∴△FAE≌△HAE(SAS),
∴EF=HE=BE+HB,
∴EF=BE+DF,
∵BE=2,DF=6,
∴EF=2+6=8.
故答案为:8.
点评:本题主要考查正方形的性质,旋转的性质,全等三角形的判定以及性质.作出辅助线延长EB至H,使BH=DF,利用全等三角形性质与判定求出是解题关键.

练习册系列答案
相关题目
 如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O上,∠ADC=65°,则∠BAC=
如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O上,∠ADC=65°,则∠BAC=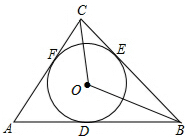 如图,圆O与△ABC的三边分别相切于点D,E,F,连接OB,OC,求证:∠BOC=90°-
如图,圆O与△ABC的三边分别相切于点D,E,F,连接OB,OC,求证:∠BOC=90°-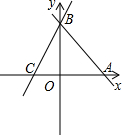 直线AB:y=-x-b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.
直线AB:y=-x-b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.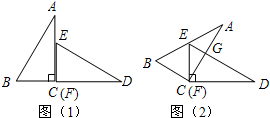 如图,已知△ACB与△DFE是两个全等的直角三角形,量得它们的斜边长为10cm,较小锐角为30°,将这两个三角形摆成如图(1)所示的形状,使点B、C、F、D在同一条直线上,且点C与点F重合,将图(1)中的△ACB绕点C顺时针方向旋转到图(2)的位置,点E在AB边上,AC交DE于点G,则BD之间的距离为
如图,已知△ACB与△DFE是两个全等的直角三角形,量得它们的斜边长为10cm,较小锐角为30°,将这两个三角形摆成如图(1)所示的形状,使点B、C、F、D在同一条直线上,且点C与点F重合,将图(1)中的△ACB绕点C顺时针方向旋转到图(2)的位置,点E在AB边上,AC交DE于点G,则BD之间的距离为 如图,PB⊥AB,PC⊥AC,PB=PC,D是AP上一点.求证:∠BDP=∠CDP.
如图,PB⊥AB,PC⊥AC,PB=PC,D是AP上一点.求证:∠BDP=∠CDP.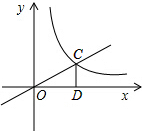 如图,已知正比例函数y=kx(k≠0)的图象与反比例函数y=
如图,已知正比例函数y=kx(k≠0)的图象与反比例函数y= 如图,在△ABC中,BA=BC,D,E是AC边上的两点,且满足∠DBE=
如图,在△ABC中,BA=BC,D,E是AC边上的两点,且满足∠DBE=