题目内容
已知,如图,在△ABC中,∠B=2∠C,AD是△ABC的角平分线,请说明AC=AB+BD.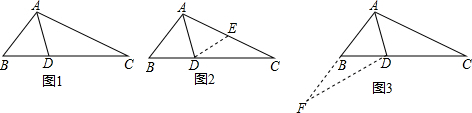
方法一:截长法:(图2)
在较长的线段上截一条线段等于较短线段.
方法二:补短法:(图3)
延长较短线段和较长线段相等.

方法一:截长法:(图2)
在较长的线段上截一条线段等于较短线段.
方法二:补短法:(图3)
延长较短线段和较长线段相等.
考点:全等三角形的判定与性质
专题:
分析:方法一、在AC上截取AE=AB,连接DE,根据SAS推出△BAD≌△EAD,根据全等三角形的性质得出BD=DE,∠B=∠AED,求出∠C=∠EDC,推出DE=EC=BD即可;方法二、如图3,延长AB到F,使AF=AC,连接DF,根据SAS推出△FAD≌△CAD,根据全等得出∠C=∠F,求出∠F=∠BDF,推出BD=BF即可.
解答:解:方法一、在AC上截取AE=AB,连接DE,
∵AD是△ABC的角平分线,
∴∠BAD=∠EAD,
在△BAD和△EAD中
∴△BAD≌△EAD,
∴BD=DE,∠B=∠AED,
∵∠B=2∠C,∠AED=∠C+∠EDC,
∴∠C=∠EDC,
∴DE=EC=BD,
∴AC=AE+CE=AB+BD;
方法二、如图3,延长AB到F,使AF=AC,连接DF,
∵在△FAD和△CAD中
∴△FAD≌△CAD,
∴∠C=∠F,
∵∠ABC=2∠C,∠ABC=∠F+∠BDF,
∴∠F=∠BDF,
∴BD=BF,
∴AC=AF=AB+BD.
∵AD是△ABC的角平分线,
∴∠BAD=∠EAD,
在△BAD和△EAD中
|
∴△BAD≌△EAD,
∴BD=DE,∠B=∠AED,
∵∠B=2∠C,∠AED=∠C+∠EDC,
∴∠C=∠EDC,
∴DE=EC=BD,
∴AC=AE+CE=AB+BD;
方法二、如图3,延长AB到F,使AF=AC,连接DF,
∵在△FAD和△CAD中
|
∴△FAD≌△CAD,
∴∠C=∠F,
∵∠ABC=2∠C,∠ABC=∠F+∠BDF,
∴∠F=∠BDF,
∴BD=BF,
∴AC=AF=AB+BD.
点评:本题考查了全等三角形的性质和判定,三角形的外角性质的应用,解此题的关键是能正确作出辅助线,注意有两种方法:截长法和补短法.

练习册系列答案
相关题目

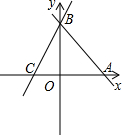 直线AB:y=-x-b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.
直线AB:y=-x-b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1. 如图,PB⊥AB,PC⊥AC,PB=PC,D是AP上一点.求证:∠BDP=∠CDP.
如图,PB⊥AB,PC⊥AC,PB=PC,D是AP上一点.求证:∠BDP=∠CDP.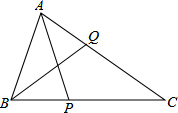 △ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交BC于P,BQ平分∠ABC交AC于Q,求证:AB+BP=BQ+AQ.(有多种辅助线作法)
△ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交BC于P,BQ平分∠ABC交AC于Q,求证:AB+BP=BQ+AQ.(有多种辅助线作法)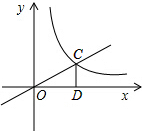 如图,已知正比例函数y=kx(k≠0)的图象与反比例函数y=
如图,已知正比例函数y=kx(k≠0)的图象与反比例函数y= 如图所示,是某市某天的气温随时间变化的图象,则由图象可知,该天最高气温与最低气温之差为
如图所示,是某市某天的气温随时间变化的图象,则由图象可知,该天最高气温与最低气温之差为