题目内容

如图是用两种正多边形密铺的平面图形图案中的一部分，其中一种是正方形，另一种与正方形相邻的四个正多边形是全等图形，那么这种正多边形是（　　）
A、正五边形、轴对称图形
B、正六边形、中心对称图形
C、正七边形、轴对称图形
D、正八边形、中心对称图形
考点：平面镶嵌（密铺）,轴对称图形,中心对称图形
专题：
分析：正八边形的每个内角为：180°-360°÷8=135°，利用“围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角”作为相等关系列出多边形个数之间的数量关系，利用多边形的个数都是正整数可推断出能和正八边形一起密铺的多边形是正四边形．
解答：解：正四边形的每个内角是90°，得90°+2×135°=360°，所以能铺满，
即用两种正多边形密铺的平面图形图案中的一部分，其中一种是正方形，
另一种与正方形相邻的四个正多边形是全等图形，那么这种正多边形是正八边形，这个图形是中心对称图形．
故选：D．
点评：此题主要考查了平面镶嵌以及中心对称图形的定义，正确把握平面镶嵌的定义是解题关键．
练习册系列答案
相关题目
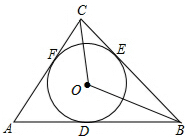如图，圆O与△ABC的三边分别相切于点D，E，F，连接OB，OC，求证：∠BOC=90°-
1
2
∠A．
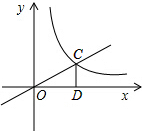如图，已知正比例函数y=kx（k≠0）的图象与反比例函数y=
m
x
（m≠0）的图象在第一象限内交于C点，CD⊥x轴，垂足为点D，若CD=OD，OC=
2
．
（1）求正比例函数和反比例函数的解析式．
（2）在第一象限的反比例函数图象上求出点P，使S△ODP=2S△ODC．
点M在△ABC的BC的边上，把以点M为圆心的⊙M称之为△ABC的伴随圆．在△ABC中，∠BAC=90°，AB=4，AC=8，M是BC边的中点．
（1）如图1，当MN⊥BC交AC于点N时，求线段MN的长；
（2）如图2，当△ABC的伴随圆⊙M与△ABC一边相切时，求出他们重叠部分的面积；
（3）如图3，设伴随圆⊙M的半径为R，请直接写出△ABC的边与⊙M的公共点个数所有可能的情况，并写出相应的R的取值范围．
在正方形的四个顶点处标上“平安临海“四个字，将正方形放置在数轴上，其中“临““海“对应的数分别为-2和-1，现将正方形绕着顶点顺时针方向在数轴上向右无滑动的翻滚，例如第一次翻滚后“平“所对应的数为0，则连续翻滚后数轴上数2014对应的字是
 
．
若反比例函数y=
2
x
与一次函数y=x-3的图象的交点坐标（a，b），则式子
1
a
-
1
b
的值为
 
．
如图，在△ABC中，BA=BC，D，E是AC边上的两点，且满足∠DBE=
1
2
∠ABC（0°＜∠CBE＜
1
2
∠ABC），以点B为旋转中心，将△BEC按逆时针旋转，得到△BE′A（点C与点A重合，点E到点E′处）连接DE′，求证：DE′=DE．
已知A（-
1
2
，y1）、B（-1，y2）在函数y=
9
x
的图象上，则y1、y2的大小关系是
 
．
下列说法中：①过两点有且只有一条直线，②连接两点的线段为两点的距离，③一个锐角的补角比它的余角大90°，④正方体的三视图相同，其中正确的个数有（　　）
A、4个B、3个C、2个D、1个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网