题目内容
9.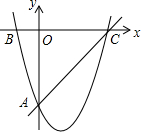 如图,已知二次函数y1=$\frac{1}{2}$x2+bx+c的图象与x轴交于B(-2,0)、C两点,与y轴交于点A(0,-6),直线AC的函数解析式为y2=mx+n
如图,已知二次函数y1=$\frac{1}{2}$x2+bx+c的图象与x轴交于B(-2,0)、C两点,与y轴交于点A(0,-6),直线AC的函数解析式为y2=mx+n(1)求二次函数的解析式及顶点坐标;
(2)过线段OC上任意一点(不含端点)作y轴的平行线,交AC于点E与二次函数图象交于点F,求线段EF的最大值;
(3)在抛物线上是否存在一点P,△ACP是以AC为底边的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
分析 (1)将A(0,-6),B(-2,0)代入y1=$\frac{1}{2}$x2+bx+c,得到关于b、c的二元一次方程组,求解即可得到二次函数的解析式;再利用配方法把一般式化为顶点式,即可求出顶点坐标;
(2)先根据抛物线的对称性求出C点坐标,利用待定系数法求出直线AC的函数解析式,再设E(x,x-6),则F(x,$\frac{1}{2}$x2-2x-6),用含x的代数式表示EF,然后根据二次函数的性质即可求出EF的最大值;
(3)假设在抛物线上存在一点P,△ACP是以AC为底边的等腰三角形.先根据中点坐标公式求出AC中点Q的坐标,再根据等腰三角形三线合一的性质得出PQ⊥AC,由互相垂直的两直线斜率之积为-1得到直线PQ的斜率是-1,再求出直线PQ的解析式,将它与二次函数的解析式联立得到方程组,求出方程组的解即可.
解答 解:(1)∵二次函数y1=$\frac{1}{2}$x2+bx+c的图象过点A(0,-6),B(-2,0),
∴$\left\{\begin{array}{l}{c=-6}\\{2-2b+c=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=-2}\\{c=-6}\end{array}\right.$,
∴二次函数的解析式为y1=$\frac{1}{2}$x2-2x-6;
∵y1=$\frac{1}{2}$x2-2x-6=$\frac{1}{2}$(x2-4x+4)-2-6=$\frac{1}{2}$(x-2)2-8,
∴顶点坐标为(2,-8);
(2)∵y1=$\frac{1}{2}$x2-2x-6的对称轴为直线x=2,
B(-2,0)与C关于直线x=2对称,
∴C(6,0).
将A(0,-6),C(6,0)代入直线AC的函数解析式y2=mx+n,
得$\left\{\begin{array}{l}{n=-6}\\{6m+n=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=1}\\{n=-6}\end{array}\right.$,
∴直线AC的函数解析式y2=x-6.
设E(x,x-6),则F(x,$\frac{1}{2}$x2-2x-6),
∵0<x<6,
∴EF=(x-6)-($\frac{1}{2}$x2-2x-6)=-$\frac{1}{2}$x2+3x=-$\frac{1}{2}$(x-3)2+$\frac{9}{2}$,
∴当x=3时,EF有最大值$\frac{9}{2}$;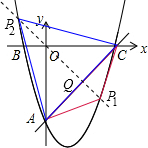 (3)假设在抛物线上存在一点P,△ACP是以AC为底边的等腰三角形.
(3)假设在抛物线上存在一点P,△ACP是以AC为底边的等腰三角形.
如图,设AC中点是Q.
∵A(0,-6),C(6,0),
∴Q(3,-3).
∵PA=PC,AQ=CQ,
∴PQ⊥AC,
∴直线PQ的斜率是-1,
设直线PQ的解析式为y=-x+t,
把Q(3,-3)代入,得-3=-3+t,解得t=0,
∴直线PQ的解析式为y=-x.
由方程组$\left\{\begin{array}{l}{y=-x}\\{y=\frac{1}{2}{x}^{2}-2x-6}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1+\sqrt{13}}\\{y=-1-\sqrt{13}}\end{array}\right.$,$\left\{\begin{array}{l}{x=1-\sqrt{13}}\\{y=-1+\sqrt{13}}\end{array}\right.$,
故所求点P的坐标为P1(1+$\sqrt{13}$,-1-$\sqrt{13}$),P2(1-$\sqrt{13}$,-1+$\sqrt{13}$).
点评 本题是二次函数综合题,其中涉及到利用待定系数法求一次函数、二次函数的解析式,函数图象上点的坐标特征,二次函数的性质,中点坐标公式,等腰三角形的性质,互相垂直的两直线斜率之积为-1,两函数交点坐标的求法等知识,综合性较强,难度适中.利用数形结合与方程思想是解题的关键.

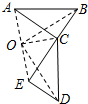 如图,△ABC绕着点O按顺时针方向旋转90°后到达了△CDE的位置,下列说法中不正确的是( )
如图,△ABC绕着点O按顺时针方向旋转90°后到达了△CDE的位置,下列说法中不正确的是( )| A. | AB⊥CD | B. | AC⊥CE | ||
| C. | BC⊥DE | D. | 点C与点C是两个三角形的对应点 |
 如图所示的几何体是由六个小正方体组合而成的,它的左视图是( )
如图所示的几何体是由六个小正方体组合而成的,它的左视图是( )



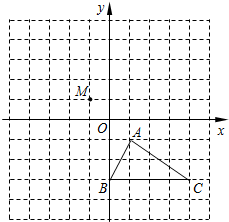 在如图所示的正方形网格中,△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,-1).
在如图所示的正方形网格中,△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,-1).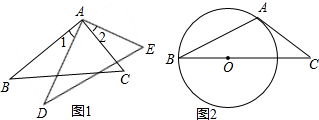
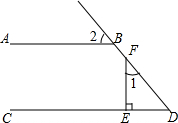 如图,AB∥CD,FE⊥CD,垂足为E,∠1=40°,则∠2的度数是50°.
如图,AB∥CD,FE⊥CD,垂足为E,∠1=40°,则∠2的度数是50°.