题目内容
2.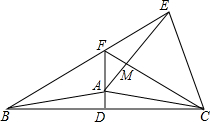 已知:如图,在等腰三角形ABC中,120°<∠BAC<180°,AB=AC,AD⊥BC于点D.以AC为边作等边三角形ACE,△ACE与△ABC在直线AC的异侧,直线BE交直线AD于点F,连接FC交AE于点M.
已知:如图,在等腰三角形ABC中,120°<∠BAC<180°,AB=AC,AD⊥BC于点D.以AC为边作等边三角形ACE,△ACE与△ABC在直线AC的异侧,直线BE交直线AD于点F,连接FC交AE于点M. (1)求证:∠FEA=∠FCA;
(2)猜想线段FE,FA,FD之间的数量关系,并证明你的结论.
分析 (1)根据等腰三角形的性质得出∠1=∠2,直线AD垂直平分BC,求出FB=FC,根据等腰三角形的性质得出∠3=∠4,求出AB=AE,根据等腰三角形的性质得出∠3=∠5,即可得出答案;
(2)在FC上截取FN,使FN=FE,连接EN,求出∠EFM=∠CAM,根据等边三角形的性质得出∠EFM=60°,根据等边三角形的判定得出△EFN是等边三角形,求出∠FEN=60°,EN=EF,求出∠5=∠6,根据SAS推出△EFA≌△ENC,根据全等得出FA=NC,求出FC=2FD,即可得出答案.
解答 (1)证明:如图1,
∵AB=AC,
∴∠1=∠2,
∵AD⊥BC,
∴直线AD垂直平分BC,
∴FB=FC,
∴∠FBC=∠FCB,
∴∠FBC-∠1=∠FCB-∠2,
即∠3=∠4,
∵等边三角形ACE中,AC=AE,
∴AB=AE,
∴∠3=∠5,
∴∠4=∠5,
即∠FEA=∠FCA;
(2)FE+FA=2FD,
证明:在FC上截取FN,使FN=FE,连接EN,如图2,
∵∠FME=∠AMC,∠5=∠4,
∴180°-∠5-∠FME=180°-∠4-∠AMC,
∴∠EFM=∠CAM,
∵等边三角形ACE中,∠CAE=60°,
∴∠EFM=60°,
∵FN=FE,
∴△EFN是等边三角形,
∴∠FEN=60°,EN=EF,
∵△ACE为等边三角形,
∴∠AEC=60°,EA=EC,
∴∠FEN=∠AEC,
∴∠FEN-∠MEN=∠AEC-∠MEN,
即∠5=∠6,
在△EFA和∠ENC中,
$\left\{\begin{array}{l}{EF=EN}\\{∠5=∠6}\\{EA=EC}\end{array}\right.$
∴△EFA≌△ENC,
∴FA=NC,
∴FE+FA=FN+NC=FC,
∵∠EFC=∠FBC+∠FCB=60°,∠FBC=∠FCB,
∴∠FCB=$\frac{1}{2}×$60°=30°,
∵AD⊥BC,
∴∠FDC=90°,
∴FC=2FD,
∴FE+FA=2FD.
点评 本题考查了等腰三角形的性质,等边三角形的性质和判定,含30°角的直角三角形的性质,全等三角形的性质和判定的应用,能综合运用知识点进行推理是解此题的关键,难度偏大.

 如图,平面直角坐标系中,△ABC的顶点坐标分别是A(-3,1),B(-1,1),C(-2,2),当直线y﹦-$\frac{1}{2}$x+b与△ABC有公共点时,b的取值范围是( )
如图,平面直角坐标系中,△ABC的顶点坐标分别是A(-3,1),B(-1,1),C(-2,2),当直线y﹦-$\frac{1}{2}$x+b与△ABC有公共点时,b的取值范围是( )| A. | -1≤b≤$\frac{1}{2}$ | B. | -1≤b≤1 | C. | -$\frac{1}{2}$≤b≤1 | D. | -$\frac{1}{2}$≤b≤$\frac{1}{2}$ |
| A. | 3 | B. | 4 | C. | -3 | D. | ±3 |
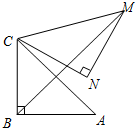 如图,Rt△ABC中,∠ABC=90°,AB=BC=2,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,那么BM的长是$\sqrt{6}+\sqrt{2}$.
如图,Rt△ABC中,∠ABC=90°,AB=BC=2,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,那么BM的长是$\sqrt{6}+\sqrt{2}$.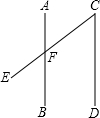 如图,AB∥CD,∠AFE=125°,则∠C的度数为55°.
如图,AB∥CD,∠AFE=125°,则∠C的度数为55°.



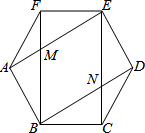 如图,在正六边形ABCDEF中,对角线AE与BF相交于点M,BD与CE相交于点N.
如图,在正六边形ABCDEF中,对角线AE与BF相交于点M,BD与CE相交于点N.