题目内容
12.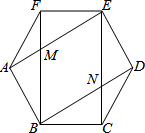 如图,在正六边形ABCDEF中,对角线AE与BF相交于点M,BD与CE相交于点N.
如图,在正六边形ABCDEF中,对角线AE与BF相交于点M,BD与CE相交于点N.(1)观察图形,写出图中与△ABM全等三角形;
(2)选择(1)中的一对全等三角形加以证明.
分析 (1)先证明△ABM≌△DEN,同理得出△ABM≌△FEM≌△CBN,
(2)选择△ABM≌△DEN证明,根据正六边形得出∠ABM=∠DEN,AB=DE,∠BAM=∠EDN,证明全等即可.
解答 解:(1)与△ABM全等的三角形有△DEN,△FEM≌△CBN;
(2)证明△ABM≌△DEN,
证明:∵六边形ABCDEF是正六边形,
∴AB=DE,∠BAF=120°,
∴∠ABM=30°,
∴∠BAM=90°,
同理∠DEN=30°,∠EDN=90°,
∴∠ABM=∠DEN,∠BAM=∠EDN,
在△ABM和△DEN中,
$\left\{\begin{array}{l}{∠BAM=∠EDN}\\{AB=DE}\\{∠ABM=∠DEN}\end{array}\right.$,
∴△ABM≌△DEN(ASA).
点评 本题考查了正多边形和圆以及全等三角形的判定,掌握正多边形的性质和全等三角形的判定是解题的关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
17. 已知实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简$\sqrt{(a+b)^{2}}$-|a-b|的结果为( )
已知实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简$\sqrt{(a+b)^{2}}$-|a-b|的结果为( )
 已知实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简$\sqrt{(a+b)^{2}}$-|a-b|的结果为( )
已知实数a、b在数轴上的位置如图所示,且|a|>|b|,则化简$\sqrt{(a+b)^{2}}$-|a-b|的结果为( )| A. | 2b | B. | -2a | C. | -2b | D. | 2a |
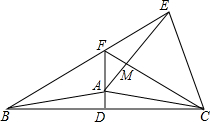 已知:如图,在等腰三角形ABC中,120°<∠BAC<180°,AB=AC,AD⊥BC于点D.以AC为边作等边三角形ACE,△ACE与△ABC在直线AC的异侧,直线BE交直线AD于点F,连接FC交AE于点M.
已知:如图,在等腰三角形ABC中,120°<∠BAC<180°,AB=AC,AD⊥BC于点D.以AC为边作等边三角形ACE,△ACE与△ABC在直线AC的异侧,直线BE交直线AD于点F,连接FC交AE于点M. 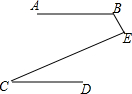 如图,AB∥CD,∠B=125°,∠C=23°,则∠E的度数为78°.
如图,AB∥CD,∠B=125°,∠C=23°,则∠E的度数为78°. 如图,四边形ABCD是菱形,AB边上的高DE长为4cm,AE=3cm,动点P从点E出发,沿折线E-B-C向终点C运动,运动速度为1cm/s.动点Q从点B出发,沿折线B-C-D向终点D运动,运动速度为2cm/s,点P、Q同时出发,当其中的一个点到达终点时,另一点也随之停止运动,设点P的运动时间为t(s)
如图,四边形ABCD是菱形,AB边上的高DE长为4cm,AE=3cm,动点P从点E出发,沿折线E-B-C向终点C运动,运动速度为1cm/s.动点Q从点B出发,沿折线B-C-D向终点D运动,运动速度为2cm/s,点P、Q同时出发,当其中的一个点到达终点时,另一点也随之停止运动,设点P的运动时间为t(s)