题目内容
15.(1)计算:(2017-π)0-($\frac{1}{3}$)-1+3sin30°(2)先化简,再求值;(1-$\frac{1}{a+1}$)÷$\frac{a}{{a}^{2}+2a+1}$,其中a=$\sqrt{3}$-1.
分析 (1)根据零指数幂、负整数指数幂、特殊角的三角函数值可以解答本题;
(2)先化简题目中的式子,然后将a的值代入化简后的式子即可解答本题.
解答 解:(1)(2017-π)0-($\frac{1}{3}$)-1+3sin30°
=1-3+3×$\frac{1}{2}$
=1-3+$\frac{3}{2}$
=$-\frac{1}{2}$;
(2)(1-$\frac{1}{a+1}$)÷$\frac{a}{{a}^{2}+2a+1}$
=$\frac{a+1-1}{a+1}×\frac{(a+1)^{2}}{a}$
=$\frac{a}{a+1}×\frac{(a+1)^{2}}{a}$
=a+1,
当a=$\sqrt{3}$-1时,原式=$\sqrt{3}-1+1=\sqrt{3}$.
点评 本题考查分式的化简求值、实数的运算、零指数幂、负整数指数幂、特殊角的三角函数值,解答本题的关键是明确它们各自的计算方法.

练习册系列答案
相关题目
6. 实数a、b在数轴上对应点如图,那么下列各式中一定为负数的是( )
实数a、b在数轴上对应点如图,那么下列各式中一定为负数的是( )
 实数a、b在数轴上对应点如图,那么下列各式中一定为负数的是( )
实数a、b在数轴上对应点如图,那么下列各式中一定为负数的是( )| A. | a+b | B. | b-a | C. | |a-b| | D. | |a|-|b| |
10.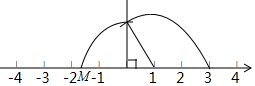 根据图中所示的作图方法,先后得到分别以表示1的点和原点为圆心的两条弧,第二条弧与数轴相交于点M,则点M所表示的数为( )
根据图中所示的作图方法,先后得到分别以表示1的点和原点为圆心的两条弧,第二条弧与数轴相交于点M,则点M所表示的数为( )
 根据图中所示的作图方法,先后得到分别以表示1的点和原点为圆心的两条弧,第二条弧与数轴相交于点M,则点M所表示的数为( )
根据图中所示的作图方法,先后得到分别以表示1的点和原点为圆心的两条弧,第二条弧与数轴相交于点M,则点M所表示的数为( )| A. | -1.7 | B. | -$\sqrt{2}$ | C. | -$\sqrt{3}$ | D. | -$\sqrt{5}$ |
20.小华通过学习函数发现:若二次函数y=ax2+bx+c(a≠0)的图象经过点(x1,y1),(x2,y2)(x1<x2),若y1y2<0,则方程ax2+bx+c=0(a≠0)的一个根x0的取值范围是x1<x0<x2,请你类比此方法,推断方程x3+x-1=0的实数根x0所在范围为( )
| A. | -$\frac{1}{2}$<x0<0 | B. | 0<x0<$\frac{1}{2}$ | C. | $\frac{1}{2}$<x0<1 | D. | 1<x0<$\frac{3}{2}$ |
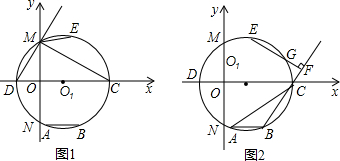
 如图,直线AB与⊙O相交于C、D两点,CE是⊙O的直径,CF平分∠BCE交⊙O于点F,过点F作FG⊥AB,垂足为点G,连接DF.
如图,直线AB与⊙O相交于C、D两点,CE是⊙O的直径,CF平分∠BCE交⊙O于点F,过点F作FG⊥AB,垂足为点G,连接DF.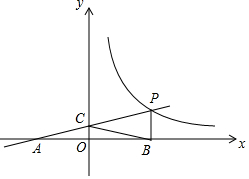 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.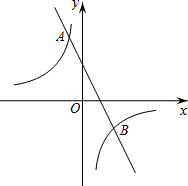 如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+2交于点A(-1,a).
如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+2交于点A(-1,a).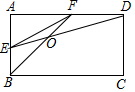 如图,在矩形ABCD中,E、F分别是AB、AD的中点,连接BF、DE交于点O,连接EF,给出如下结论:
如图,在矩形ABCD中,E、F分别是AB、AD的中点,连接BF、DE交于点O,连接EF,给出如下结论: