题目内容
7.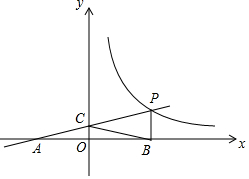 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.(1)求一次函数,反比例函数的解析式;
(2)求证:点C为线段AP的中点;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,说明理由并求出点D的坐标;如果不存在,说明理由.
分析 (1)由条件可求得P点坐标,利用待定系数法可求得一次函数和反比例函数的解析式;
(2)由平行线分线段成比例可求得AC=PC,可证得结论;
(3)可先求得C点坐标,过C作CD∥x轴,交PB于点E,交反比例函数图象于点D,可求得此时D点坐标,可证得四边形BCPD为菱形.
解答 解:
(1)∵点A与点B关于y轴对称,
∴AO=BO,
∵A(-4,0),
∴B(4,0),
∵PB⊥x轴于点B,
∴P(4,2),
把P(4,2)代入反比例函数解析式可得m=8,
∴反比例函数解析式为y=$\frac{8}{x}$,
把A、P两点坐标代入一次函数解析式可得$\left\{\begin{array}{l}{0=-4k+b}\\{2=4k+b}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{1}{4}}\\{b=1}\end{array}\right.$,
∴一次函数解析式为y=$\frac{1}{4}$x+1;
(2)证:∵点A与点B关于y轴对称,
∴OA=OB,
∵PB⊥x轴于点B,
∴∠PBA=∠COA=90°,
∴PB∥CO,
∴$\frac{OA}{OB}$=$\frac{AC}{PC}$=1,即AC=PC,
∴点C为线段AP的中点;
(3)存在点D,使四边形BCPD为菱形.
理由如下:
∵点C为线段AP的中点,
∴BC=$\frac{1}{2}$AP=PC,
∴BC和PC是菱形的两条边,
由y=$\frac{1}{4}$x+1可得C(0,1),
如图,过点C作CD∥x轴,交PB于点E,交反比例函数图象于点D,分别连接PD、BD,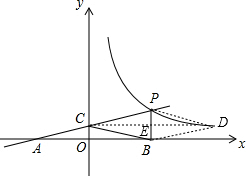
∴D(8,1),且PB⊥CD,
∴PE=BE=1,CE=DE=4,
∴PB与CD互相垂直平分,即四边形BCPD为菱形,
∴存在满足条件的点D,其坐标为(8,1).
点评 本题为反比例函数的综合应用,涉及待定系数法、平行线分线段成比例、菱形的判定和性质等知识.在(1)中求得P点坐标是解题的关键,在(2)中注意利用平行线分线段成比例是解题的关键,在(3)中确定出D点的坐标是解题的关键.本题考查知识点较多,综合性较强,难度适中.





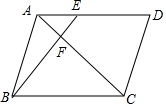 如图,点E为?ABCD中AD边上一点,且AE=$\frac{1}{2}$DE,AC与BE相交于点F,则$\frac{AF}{FC}$=$\frac{1}{3}$.
如图,点E为?ABCD中AD边上一点,且AE=$\frac{1}{2}$DE,AC与BE相交于点F,则$\frac{AF}{FC}$=$\frac{1}{3}$.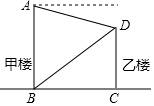 如图,在甲楼的底部B处测得乙楼的顶部D点的仰角为α,在甲楼的顶部A处测得乙楼的顶部D点的俯角为β,如果乙楼的高DC=10米,那么甲楼的高AB=$\frac{10tanβ}{tanα}$+10米(用含α,β的代数式表示)
如图,在甲楼的底部B处测得乙楼的顶部D点的仰角为α,在甲楼的顶部A处测得乙楼的顶部D点的俯角为β,如果乙楼的高DC=10米,那么甲楼的高AB=$\frac{10tanβ}{tanα}$+10米(用含α,β的代数式表示)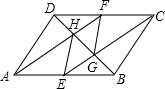 如图,已知在平行四边形ABCD中,点E、F分别是AB、CD的中点,CE、AF与对角线BD分别相交于点G、H,联结EH、FG.
如图,已知在平行四边形ABCD中,点E、F分别是AB、CD的中点,CE、AF与对角线BD分别相交于点G、H,联结EH、FG.