题目内容
3. 如图,直线AB与⊙O相交于C、D两点,CE是⊙O的直径,CF平分∠BCE交⊙O于点F,过点F作FG⊥AB,垂足为点G,连接DF.
如图,直线AB与⊙O相交于C、D两点,CE是⊙O的直径,CF平分∠BCE交⊙O于点F,过点F作FG⊥AB,垂足为点G,连接DF.(1)求证:FG是⊙O切线;
(2)已知⊙O的直径为8,CG=3,求sin∠CDF的值.
分析 (1)连接OF,由角平分线定义和等腰三角形的性质得出∠FCG=∠OFC.证出OF∥BC.由FG⊥AB,得出FG⊥OF,即可得出结论.
(2)连接EF,由圆周角定理得出∠CFE=90°,∠CDF=∠E,证明△CEF∽△CFG,得出对应边成比例求出CF=2$\sqrt{6}$;在Rt△CEF中,由三角函数定义求出sinE=$\frac{CF}{CE}$=$\frac{\sqrt{6}}{4}$,即可得出in∠CDF=$\frac{\sqrt{6}}{4}$.
解答 (1)证明: 连接OF.如图1所示:
连接OF.如图1所示:
∵CF平分∠BCE,
∴∠FCG=∠ECF.
∵OC=OF,
∴∠ECF=∠OFC,
∴∠FCG=∠OFC.
∴OF∥BC.
∵FG⊥AB,
∴FG⊥OF,
∴FG是⊙O的切线.
(2)解:连接EF.
∵CE是⊙O的直径,
∴∠CFE=90°.
∵FG⊥AB,
∴∠FGC=90°.
∵∠FCG=∠ECF,
∴△CEF∽△CFG,
∴$\frac{CG}{CF}=\frac{CF}{CE}$,即$\frac{3}{CF}=\frac{CF}{8}$.
解得:CF=2$\sqrt{6}$;
在Rt△CEF中,sinE=$\frac{CF}{CE}$=$\frac{2\sqrt{6}}{8}$=$\frac{\sqrt{6}}{4}$,
∵∠CDF=∠E,
∴sin∠CDF=$\frac{\sqrt{6}}{4}$.
点评 本题考查了切线的判定、等腰三角形的性质、圆周角定理、平行线的判定、相似三角形的判定与性质以及三角函数定义等知识;熟练掌握切线的判定和圆周角定理是解决问题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
11.下表是2016年3月份某居民小区部分居民的用电情况:
(1)画出这20户家庭3月份用电量的条形统计图;

(2)据上表中有关信息,计算或找出下表中的统计量,并将结果填入表中:
(3)如果该小区有500户家庭,根据上面的计算结果,估计该小区居民每月共用电多少度?
| 月用电量(度) | 55 | 70 | 75 | 85 | 100 | 130 |
| 户数 | 2 | 3 | 7 | 5 | 2 | 1 |

(2)据上表中有关信息,计算或找出下表中的统计量,并将结果填入表中:
| 统计量名称 | 众数 | 中位数 | 平均数 |
| 数据 | 75 | 75 | 80 |
13.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
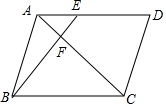 如图,点E为?ABCD中AD边上一点,且AE=$\frac{1}{2}$DE,AC与BE相交于点F,则$\frac{AF}{FC}$=$\frac{1}{3}$.
如图,点E为?ABCD中AD边上一点,且AE=$\frac{1}{2}$DE,AC与BE相交于点F,则$\frac{AF}{FC}$=$\frac{1}{3}$.


