题目内容
 如图,在△ABC中,∠B比∠BAC大35°,∠C=65°,AD平分∠BAC交AB于D,DE⊥AB于E,求∠ADE的度数.
如图,在△ABC中,∠B比∠BAC大35°,∠C=65°,AD平分∠BAC交AB于D,DE⊥AB于E,求∠ADE的度数.考点:三角形内角和定理
专题:
分析:先根据三角形内角和定理求出∠BAC的度数,再根据角平分线的定义得出∠DAB的度数,由直角三角形的性质即可得出结论.
解答:解:∵在△ABC中,∠B比∠BAC大35°,∠C=65°,
∴∠B=∠BAC+35°,
∵∠B+∠C+∠BAC=180°,即∠BAC+35°+65°+∠BAC=180°,解得∠BAC=40°.
∵AD平分∠BAC,
∴∠DAB=
∠BAC=
×40°=20°.
∵DE⊥AB,
∴∠AED=90°,
∴∠ADE=90°-20°=70°.
∴∠B=∠BAC+35°,
∵∠B+∠C+∠BAC=180°,即∠BAC+35°+65°+∠BAC=180°,解得∠BAC=40°.
∵AD平分∠BAC,
∴∠DAB=
| 1 |
| 2 |
| 1 |
| 2 |
∵DE⊥AB,
∴∠AED=90°,
∴∠ADE=90°-20°=70°.
点评:本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
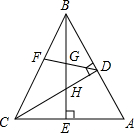 在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,F为BC中点,BE平分∠ABC,已证△BDH≌△CDA,求证:BG2-GE2=AE2.
在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,F为BC中点,BE平分∠ABC,已证△BDH≌△CDA,求证:BG2-GE2=AE2. 如图,⊙O的直径AB=4,半径OC⊥AB,D为弧BC上一点,DE⊥OC,DF⊥AB,垂足分别为E、F.则EF=
如图,⊙O的直径AB=4,半径OC⊥AB,D为弧BC上一点,DE⊥OC,DF⊥AB,垂足分别为E、F.则EF=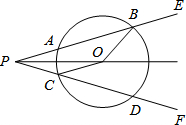 已知:如图,点O是∠EPF的平分线的一点,以O为圆心的圆和∠EPF的两边分别交于点A、B和C、D.试探究∠OBA与∠OCD的关系,并说明理由.
已知:如图,点O是∠EPF的平分线的一点,以O为圆心的圆和∠EPF的两边分别交于点A、B和C、D.试探究∠OBA与∠OCD的关系,并说明理由.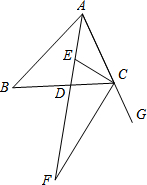 如图,△ABC中,AD为角平分线,E为AD上一点,且EC平分∠ACB,CF是△ABC的外角∠BCG的平分线,交AD延长线于F,∠F=20°,∠ACB-∠B=30°,求△ABC的三个内角的大小.
如图,△ABC中,AD为角平分线,E为AD上一点,且EC平分∠ACB,CF是△ABC的外角∠BCG的平分线,交AD延长线于F,∠F=20°,∠ACB-∠B=30°,求△ABC的三个内角的大小.