题目内容
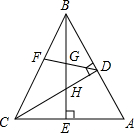 在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,F为BC中点,BE平分∠ABC,已证△BDH≌△CDA,求证:BG2-GE2=AE2.
在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,F为BC中点,BE平分∠ABC,已证△BDH≌△CDA,求证:BG2-GE2=AE2.考点:全等三角形的判定与性质,等腰三角形的判定与性质,勾股定理
专题:证明题
分析:根据三角形的内角和定理求出∠BCD=∠ABC,∠ABE=∠DCA,推出DB=CD,根据ASA证出△BEC≌△BEA,推出BC=AB,推出AE=CE,根据DB=DC和F为BC中点,得出DF垂直平分BC,推出BG=CG,在Rt△CGE中,由勾股定理即可推出答案.
解答:证明:连接CG,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵BE⊥AC,
∴∠BEA=∠BEC=90°,
∵在△BEC和△BEA中,
∴△BEC≌△BEA(ASA),
∴BC=AB,
∵BE⊥AC,
∴AE=CE,
∵CD⊥AB,
∴∠CDB=90°,
∵∠ABC=45°,
∴∠DBC=∠BCD=45°,
∴BD=CD,
∵F为BC中点,
∴DF⊥BC,
∴BG=CG,
在Rt△CGE中,由勾股定理得:CG2-GE2=CE2,
即BG2-GE2=AE2.
∵BE平分∠ABC,

∴∠ABE=∠CBE,
∵BE⊥AC,
∴∠BEA=∠BEC=90°,
∵在△BEC和△BEA中,
|
∴△BEC≌△BEA(ASA),
∴BC=AB,
∵BE⊥AC,
∴AE=CE,
∵CD⊥AB,
∴∠CDB=90°,
∵∠ABC=45°,
∴∠DBC=∠BCD=45°,
∴BD=CD,
∵F为BC中点,
∴DF⊥BC,
∴BG=CG,
在Rt△CGE中,由勾股定理得:CG2-GE2=CE2,
即BG2-GE2=AE2.
点评:本题考查了等腰三角形性质,全等三角形的性质和判定,线段的垂直平分线的性质的应用,注意:线段垂直平分线上的点到线段两端的距离相等,等腰三角形具有三线合一的性质,主要考查学生运用定理进行推理的能力.

练习册系列答案
相关题目
抛物线y=x2-4与x轴交于B,C两点,顶点为A,则△ABC的周长为( )
A、4
| ||
B、4
| ||
| C、12 | ||
D、2
|
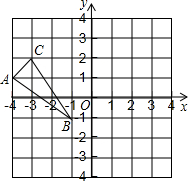 如图,△ABC三个顶点的坐标分别是A(-4,1),B(-1,-1),C(-3,2).
如图,△ABC三个顶点的坐标分别是A(-4,1),B(-1,-1),C(-3,2). 等边△ABC边长为1,D、E、F分别在边AB、BC、CA上,△DEF也是等边三角形.
等边△ABC边长为1,D、E、F分别在边AB、BC、CA上,△DEF也是等边三角形. 已知∠B=∠C=90°,M是BC的中点,MN⊥AD,若∠1=∠2,求证:∠3=∠4,你还有什么发现?
已知∠B=∠C=90°,M是BC的中点,MN⊥AD,若∠1=∠2,求证:∠3=∠4,你还有什么发现?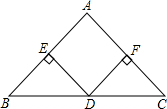 如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F.只添加一个条件,使四边形EDFA是正方形.请你至少写出两种不同的添加方法.并选择一种证明.
如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F.只添加一个条件,使四边形EDFA是正方形.请你至少写出两种不同的添加方法.并选择一种证明. 如图,在△ABC中,∠B比∠BAC大35°,∠C=65°,AD平分∠BAC交AB于D,DE⊥AB于E,求∠ADE的度数.
如图,在△ABC中,∠B比∠BAC大35°,∠C=65°,AD平分∠BAC交AB于D,DE⊥AB于E,求∠ADE的度数. 在四边形ABCD中,∠B=∠D=α.
在四边形ABCD中,∠B=∠D=α.