题目内容
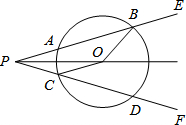 已知:如图,点O是∠EPF的平分线的一点,以O为圆心的圆和∠EPF的两边分别交于点A、B和C、D.试探究∠OBA与∠OCD的关系,并说明理由.
已知:如图,点O是∠EPF的平分线的一点,以O为圆心的圆和∠EPF的两边分别交于点A、B和C、D.试探究∠OBA与∠OCD的关系,并说明理由.考点:垂径定理,全等三角形的判定与性质,角平分线的性质
专题:
分析:过点O分别作OM⊥AB,ON⊥CD,则可知OM=ON,且OB=OC,则可证得△OMB≌△ONC,可得出∠OBA=∠OCD.
解答: 解:∠OBA=∠OCD,理由如下:
解:∠OBA=∠OCD,理由如下:
过点O分别作OM⊥AB,ON⊥CD,垂足分别为M、N
∵∠EPO=∠FPO,
∴OM=ON,
在Rt△OMB和Rt△ONC中,
,
∴Rt△OMB≌Rt△ONC(HL),
∴∠OBA=∠OCD.
 解:∠OBA=∠OCD,理由如下:
解:∠OBA=∠OCD,理由如下:过点O分别作OM⊥AB,ON⊥CD,垂足分别为M、N
∵∠EPO=∠FPO,
∴OM=ON,
在Rt△OMB和Rt△ONC中,
|
∴Rt△OMB≌Rt△ONC(HL),
∴∠OBA=∠OCD.
点评:本题主要考查全等三角形的判定和性质,正确掌握三角形全等的判定方法是解题的关键.

练习册系列答案
 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
抛物线y=x2-4与x轴交于B,C两点,顶点为A,则△ABC的周长为( )
A、4
| ||
B、4
| ||
| C、12 | ||
D、2
|
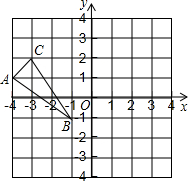 如图,△ABC三个顶点的坐标分别是A(-4,1),B(-1,-1),C(-3,2).
如图,△ABC三个顶点的坐标分别是A(-4,1),B(-1,-1),C(-3,2). 如图,在△ABC中,∠B比∠BAC大35°,∠C=65°,AD平分∠BAC交AB于D,DE⊥AB于E,求∠ADE的度数.
如图,在△ABC中,∠B比∠BAC大35°,∠C=65°,AD平分∠BAC交AB于D,DE⊥AB于E,求∠ADE的度数.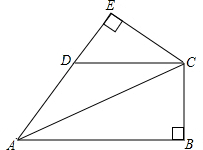 已知∠B=∠E=90°,CE=CB,AB∥CD,求证:AD=CD.
已知∠B=∠E=90°,CE=CB,AB∥CD,求证:AD=CD.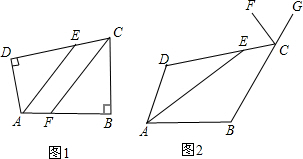 在四边形ABCD中,∠B=∠D=α.
在四边形ABCD中,∠B=∠D=α.